Hukum Coulomb adalah hukum fisika yang menggambarkan gaya tarik-menarik atau tolak-menolak antara dua muatan listrik. Hukum ini dinamai dari fisikawan Prancis, Charles-Augustin de Coulomb, yang pertama kali mempublikasikan temuan ini pada tahun 1785. Hukum Coulomb sangat penting dalam memahami interaksi antara muatan listrik dan merupakan dasar dari banyak fenomena elektromagnetik.

Dalam artikel ini, kita akan membahas secara mendetail tentang rumus Hukum Coulomb, menjelaskan konsep-konsep penting yang mendasarinya, memberikan contoh perhitungan, serta menyertakan perumpamaan sederhana untuk memudahkan pemahaman.
1. Rumus Hukum Coulomb
Hukum Coulomb menyatakan bahwa gaya antara dua muatan listrik (![]() ) sebanding dengan hasil kali besarnya muatan (
) sebanding dengan hasil kali besarnya muatan (![]() dan
dan ![]() ) dan berbanding terbalik dengan kuadrat jarak antara kedua muatan (
) dan berbanding terbalik dengan kuadrat jarak antara kedua muatan (![]() ).
).
Secara matematis, Hukum Coulomb dirumuskan sebagai:
![]()
Di mana:
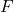 adalah gaya listrik antara dua muatan (dalam satuan Newton).
adalah gaya listrik antara dua muatan (dalam satuan Newton).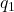 dan
dan 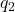 adalah besar muatan listrik dalam Coulomb (C).
adalah besar muatan listrik dalam Coulomb (C). adalah jarak antara kedua muatan (dalam meter).
adalah jarak antara kedua muatan (dalam meter).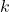 adalah konstanta Coulomb, dengan nilai
adalah konstanta Coulomb, dengan nilai 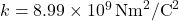 .
.
Sifat-Sifat Gaya Coulomb
- Jika kedua muatan memiliki tanda yang sama (keduanya positif atau keduanya negatif), maka gaya yang dihasilkan adalah gaya tolak-menolak.
- Jika kedua muatan memiliki tanda yang berbeda (satu positif dan satu negatif), maka gaya yang dihasilkan adalah gaya tarik-menarik.
—
2. Penjelasan Konsep Hukum Coulomb
Hukum Coulomb menjelaskan bagaimana dua benda bermuatan listrik berinteraksi satu sama lain. Interaksi ini bisa berupa gaya tarik atau gaya tolak, tergantung pada jenis muatan yang dimiliki oleh kedua benda.
a. Gaya Tolak-Menolak
Jika kedua benda memiliki muatan yang sama, misalnya keduanya bermuatan positif atau keduanya bermuatan negatif, maka mereka akan saling menolak.
b. Gaya Tarik-Menarik
Jika satu benda bermuatan positif dan benda lainnya bermuatan negatif, maka kedua benda tersebut akan saling menarik.
Perumpamaan Sederhana:
Bayangkan gaya Coulomb seperti dua magnet yang berinteraksi. Jika Anda mencoba mendekatkan dua kutub magnet yang sama (misalnya, dua kutub utara), mereka akan saling menolak. Tetapi jika Anda mendekatkan kutub yang berbeda (misalnya, kutub utara dan selatan), mereka akan saling menarik. Muatan listrik bekerja dengan cara yang mirip, meskipun sifat-sifatnya sedikit berbeda dari magnetisme.
—
3. Konstanta Coulomb (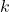 )
)
Konstanta Coulomb (![]() ) adalah faktor skala yang menentukan seberapa kuat gaya listrik yang dihasilkan oleh dua muatan. Nilainya adalah:
) adalah faktor skala yang menentukan seberapa kuat gaya listrik yang dihasilkan oleh dua muatan. Nilainya adalah:
![]()
Ini adalah angka yang sangat besar, yang menunjukkan bahwa gaya listrik antara muatan bisa sangat kuat jika jaraknya cukup dekat, bahkan jika muatan relatif kecil.
—
4. Contoh Soal Hukum Coulomb
Mari kita coba menghitung gaya listrik menggunakan Hukum Coulomb dengan contoh sederhana.
Contoh 1: Dua Muatan Saling Tolak-Menolak
Dua benda bermuatan positif, masing-masing memiliki muatan sebesar ![]() (mikroCoulomb,
(mikroCoulomb, ![]() ), terpisah sejauh 0.05 meter. Hitung gaya tolak-menolak antara kedua muatan tersebut.
), terpisah sejauh 0.05 meter. Hitung gaya tolak-menolak antara kedua muatan tersebut.
Diketahui:
Penyelesaian:
Masukkan nilai-nilai tersebut ke dalam rumus Hukum Coulomb:
![]()
![]()
![]()
![]()
![]()
Jadi, gaya tolak-menolak antara kedua muatan adalah sekitar 14.38 Newton.
Contoh 2: Dua Muatan Saling Tarik-Menarik
Dua benda bermuatan, satu bermuatan ![]() dan yang lain bermuatan
dan yang lain bermuatan ![]() , terpisah sejauh 0.1 meter. Hitung gaya tarik-menarik antara kedua muatan tersebut.
, terpisah sejauh 0.1 meter. Hitung gaya tarik-menarik antara kedua muatan tersebut.
Diketahui:
Penyelesaian:
Masukkan nilai-nilai tersebut ke dalam rumus Hukum Coulomb:
![]()
![]()
![]()
![]()
![]()
Jadi, gaya tarik-menarik antara kedua muatan adalah sekitar 10.79 Newton.
—
5. Faktor-Faktor yang Mempengaruhi Gaya Coulomb
Beberapa faktor penting yang mempengaruhi besar gaya Coulomb adalah:
a. Besar Muatan
Semakin besar nilai muatan ![]() dan
dan ![]() , semakin besar gaya yang terjadi. Artinya, jika salah satu atau kedua muatan diperbesar, gaya tarik atau tolak akan meningkat.
, semakin besar gaya yang terjadi. Artinya, jika salah satu atau kedua muatan diperbesar, gaya tarik atau tolak akan meningkat.
b. Jarak Antar Muatan
Semakin dekat jarak antara dua muatan, semakin besar gaya yang dihasilkan. Sebaliknya, semakin jauh jarak antara dua muatan, semakin kecil gaya yang bekerja. Hukum Coulomb menyatakan bahwa gaya berbanding terbalik dengan kuadrat jarak—artinya jika jarak ditingkatkan dua kali lipat, gaya akan berkurang menjadi seperempatnya.
c. Jenis Muatan
Muatan yang sama (positif-positif atau negatif-negatif) akan menghasilkan gaya tolak-menolak, sedangkan muatan yang berbeda (positif-negatif) akan menghasilkan gaya tarik-menarik.
—
6. Perumpamaan Sederhana untuk Memahami Hukum Coulomb
Bayangkan Anda memiliki dua balon yang bermuatan listrik. Jika Anda menggosok keduanya dengan kain wol (sehingga keduanya bermuatan positif), mereka akan saling menjauh—ini adalah gaya tolak-menolak. Tetapi, jika satu balon bermuatan positif dan balon lain bermuatan negatif, mereka akan saling mendekat—ini adalah gaya tarik-menarik.
Interaksi antara dua muatan ini mirip dengan bagaimana dua balon bermuatan listrik berperilaku. Jika jarak antara balon-balonnya dekat, efek tarik atau tolak akan sangat kuat. Namun, jika Anda menjauhkannya, gaya tarik atau tolak akan melemah.
—
7. Aplikasi Hukum Coulomb dalam Kehidupan Sehari-hari
Hukum Coulomb tidak hanya berlaku dalam teori fisika, tetapi juga memiliki banyak aplikasi dalam kehidupan sehari-hari dan teknologi modern:
a. Kapasitor
Hukum Coulomb berperan penting dalam prinsip kerja kapasitor, perangkat yang menyimpan energi listrik dalam medan listrik. Kapasitor digunakan dalam berbagai perangkat elektronik, mulai dari komputer hingga ponsel.
b. Pengendalian Elektrostatis
Di pabrik industri, Hukum Coulomb digunakan untuk mengendalikan muatan elektrostatis yang dapat menyebabkan ledakan atau kerusakan pada perangkat elektronik. Dengan memahami interaksi muatan, perusahaan dapat mencegah terjadinya akumulasi listrik statis yang berbahaya.
c. Pengendalian Partikel Bermuatan
Dalam teknologi seperti pencetakan laser atau fotokopi, partikel bermuatan digunakan untuk menciptakan gambar di atas kertas. Hukum Coulomb membantu menjelaskan bagaimana partikel bermuatan dapat diarahkan dan dikendalikan dengan medan listrik.
—
8. Kesimpulan
Hukum Coulomb menjelaskan gaya tarik-menarik atau tolak-menolak antara dua muatan listrik, dan dinyatakan dalam rumus ![]() . Gaya ini sebanding dengan hasil kali muatan-muatan tersebut dan berbanding terbalik dengan kuadrat jarak antara mereka. Muatan yang sama akan saling menolak, sementara muatan yang berbeda akan saling menarik.
. Gaya ini sebanding dengan hasil kali muatan-muatan tersebut dan berbanding terbalik dengan kuadrat jarak antara mereka. Muatan yang sama akan saling menolak, sementara muatan yang berbeda akan saling menarik.
Dengan perumpamaan sederhana seperti balon bermuatan yang saling menarik atau menolak, kita dapat dengan mudah memahami bagaimana gaya listrik bekerja dalam kehidupan sehari-hari. Hukum ini memiliki banyak aplikasi praktis, mulai dari teknologi elektronik hingga pengendalian elektrostatis dalam industri.
