Tag: Gerak Parabola: Karakteristik dan Contoh dalam Kehidupan Sehari-hari

Gerak parabola adalah salah satu jenis gerakan yang terjadi ketika suatu objek dilemparkan dengan kecepatan awal tertentu dan dipengaruhi oleh gaya gravitasi. Gerakan ini menghasilkan lintasan berbentuk parabola, yang merupakan kurva simetris. Gerak parabola sering kali terjadi dalam berbagai situasi sehari-hari, seperti saat melempar bola, menembakkan proyektil, atau saat air yang disemprot dari selang. Dalam artikel ini, kita akan membahas secara mendetail tentang pengertian gerak parabola, karakteristiknya, rumus-rumus yang terkait, serta contoh-contoh dalam kehidupan sehari-hari, disertai dengan penjelasan ilustratif untuk setiap konsep.

Pengertian Gerak Parabola

Gerak parabola adalah gerakan suatu objek yang bergerak dalam dua dimensi, di mana objek tersebut dilemparkan dengan sudut tertentu terhadap horizontal dan dipengaruhi oleh gaya gravitasi. Lintasan yang dihasilkan oleh gerakan ini berbentuk parabola. Gerak parabola dapat dianalisis dengan memisahkan komponen horizontal dan vertikal dari gerakan tersebut.

  • Ilustrasi: Bayangkan gerak parabola sebagai “jalur peluru.” Seperti peluru yang ditembakkan dari senapan, lintasan peluru membentuk kurva parabola saat bergerak di udara.

Karakteristik Gerak Parabola

Gerak parabola memiliki beberapa karakteristik penting yang membedakannya dari jenis gerakan lainnya. Berikut adalah beberapa karakteristik utama dari gerak parabola:

1. Lintasan Berbentuk Parabola

Lintasan gerak parabola berbentuk kurva simetris yang disebut parabola. Bentuk ini dihasilkan dari kombinasi gerakan horizontal yang konstan dan gerakan vertikal yang dipengaruhi oleh percepatan gravitasi.

  • Ilustrasi: Bayangkan lintasan parabola sebagai “jembatan melengkung.” Seperti jembatan yang membentuk lengkungan, lintasan gerak parabola juga membentuk kurva.

2. Kecepatan Horizontal Konstan

Dalam gerak parabola, komponen kecepatan horizontal tetap konstan karena tidak ada gaya yang bekerja pada arah horizontal (asumsi tidak ada hambatan udara). Ini berarti objek bergerak dengan kecepatan yang sama sepanjang lintasan horizontal.

  • Ilustrasi: Bayangkan kecepatan horizontal sebagai “kereta yang melaju di rel.” Seperti kereta yang bergerak dengan kecepatan tetap di atas rel, objek dalam gerak parabola memiliki kecepatan horizontal yang konstan.

3. Percepatan Vertikal Konstan

Komponen kecepatan vertikal objek berubah seiring waktu karena pengaruh gaya gravitasi. Percepatan vertikal adalah konstan dan memiliki nilai sekitar 9,8 m/s² (di permukaan bumi), yang menyebabkan objek mengalami perlambatan saat naik dan percepatan saat jatuh.

  • Ilustrasi: Bayangkan percepatan vertikal sebagai “gaya tarik bumi.” Seperti magnet yang menarik benda ke bawah, gaya gravitasi menarik objek ke arah tanah.

Rumus-Rumus Gerak Parabola

Dalam gerak parabola, terdapat beberapa rumus yang digunakan untuk menghitung berbagai aspek gerakan. Berikut adalah rumus-rumus utama yang terkait dengan gerak parabola:

1. Jarak Horizontal (Jarak Tempuh)

Jarak horizontal (R) yang ditempuh oleh objek dalam gerak parabola dapat dihitung dengan rumus:

    \[ R = v_0 \cdot \cos(\theta) \cdot t \]

Di mana:

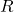  • R = jarak horizontal (m)
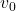  • v_0 = kecepatan awal (m/s)
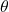  • \theta = sudut lemparan (derajat)
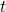  • t = waktu total (s)
  • Ilustrasi: Bayangkan jarak horizontal sebagai “panjang jembatan.” Seperti jembatan yang menghubungkan dua tepi sungai, jarak horizontal menunjukkan seberapa jauh objek bergerak di sepanjang sumbu horizontal.

2. Tinggi Maksimum

Tinggi maksimum (H) yang dicapai oleh objek dalam gerak parabola dapat dihitung dengan rumus:

    \[ H = \frac{v_0^2 \cdot \sin^2(\theta)}{2g} \]

Di mana:

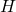  • H = tinggi maksimum (m)
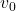  • v_0 = kecepatan awal (m/s)
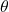  • \theta = sudut lemparan (derajat)
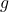  • g = percepatan gravitasi (m/s²)
  • Ilustrasi: Bayangkan tinggi maksimum sebagai “puncak gunung.” Seperti gunung yang memiliki puncak tertinggi, tinggi maksimum menunjukkan seberapa tinggi objek dapat mencapai sebelum mulai jatuh.

3. Waktu Total

Waktu total (T) yang diperlukan untuk objek mencapai tanah setelah dilemparkan dapat dihitung dengan rumus:

    \[ T = \frac{2v_0 \cdot \sin(\theta)}{g} \]

  • Ilustrasi: Bayangkan waktu total sebagai “lama perjalanan.” Seperti waktu yang dibutuhkan untuk mendaki dan menuruni gunung, waktu total menunjukkan berapa lama objek berada di udara.

Contoh Gerak Parabola dalam Kehidupan Sehari-hari

Gerak parabola dapat ditemukan dalam berbagai situasi dalam kehidupan sehari-hari. Berikut adalah beberapa contoh yang umum:

1. Melempar Bola

Ketika kita melempar bola ke atas dengan sudut tertentu, bola tersebut mengalami gerak parabola. Misalnya, jika kita melempar bola dengan kecepatan awal 15 m/s pada sudut 30 derajat, kita dapat menghitung jarak horizontal yang ditempuh, tinggi maksimum yang dicapai, dan waktu total yang diperlukan.

  • Ilustrasi: Bayangkan bola sebagai “pemain yang berusaha mencetak gol.” Seperti pemain yang melempar bola ke arah gawang, bola mengalami gerak parabola saat dilempar.

2. Menembakkan Proyektil

Ketika sebuah proyektil ditembakkan dari senapan, lintasan proyektil tersebut juga membentuk parabola. Misalnya, jika proyektil ditembakkan dengan kecepatan awal 200 m/s pada sudut 45 derajat, kita dapat menghitung jarak horizontal yang ditempuh dan tinggi maksimum yang dicapai.

  • Ilustrasi: Bayangkan proyektil sebagai “peluru yang meluncur.” Seperti peluru yang ditembakkan dari senapan, proyektil mengalami gerak parabola saat meluncur di udara.

3. Air yang Disemprot dari Selang

Ketika kita menyemprotkan air dari selang, aliran air membentuk lintasan parabola. Misalnya, jika kita menyemprotkan air dengan kecepatan awal 10 m/s pada sudut 60 derajat, kita dapat menghitung tinggi maksimum yang dicapai air dan jarak horizontal yang ditempuh.

  • Ilustrasi: Bayangkan air sebagai “aliran yang melengkung.” Seperti aliran air yang membentuk lengkungan saat disemprotkan, air mengalami gerak parabola saat keluar dari selang.

Kesimpulan

Gerak parabola adalah konsep penting dalam fisika yang menggambarkan gerakan objek yang dilemparkan dengan sudut tertentu dan dipengaruhi oleh gaya gravitasi. Dengan memahami pengertian, karakteristik, rumus-rumus, dan contoh-contoh gerak parabola, kita dapat lebih menghargai dinamika gerakan dalam berbagai aspek kehidupan. Seperti bola yang dilempar atau proyektil yang ditembakkan, gerak parabola adalah bagian integral dari pengalaman sehari-hari kita. Kesadaran akan pentingnya gerak parabola dapat mendorong kita untuk lebih memahami prinsip-prinsip fisika yang mendasari gerakan di sekitar kita.

Kecepatan Maksimum dalam Gerak Parabola

Fisika

Gerak parabola adalah salah satu jenis gerak yang sering kita temui dalam kehidupan sehari-hari, seperti saat kita melempar bola, menembakkan proyektil, atau bahkan dalam peluncuran roket. Salah satu aspek yang sangat menarik dalam gerak ini adalah kecepatan maksimum, yaitu momen ketika suatu benda memiliki energi kinetik tertinggi dalam lintasannya. Memahami kecepatan maksimum dalam gerak parabola […]

Aplikasi Gerak Parabola dalam Kehidupan Sehari-hari

Fisika

Gerak parabola adalah salah satu konsep dalam fisika yang sangat umum kita temui dalam kehidupan sehari-hari, meskipun seringkali kita tidak menyadari bahwa fenomena tersebut mengikuti lintasan parabola. Gerak parabola adalah gerakan suatu benda yang dilempar atau ditembakkan dengan sudut tertentu terhadap bidang horizontal, di mana benda tersebut dipengaruhi oleh percepatan gravitasi. Akibatnya, lintasan benda ini […]