Momentum sudut, juga dikenal sebagai momentum rotasi, adalah konsep penting dalam fisika yang menggambarkan gerakan rotasi suatu objek. Seperti halnya momentum linier yang mengukur gerakan translasi, momentum sudut mengukur gerakan rotasi dan memiliki aplikasi yang luas dalam berbagai bidang, termasuk mekanika, astrofisika, dan teknik. Dalam artikel ini, kita akan membahas secara mendalam tentang pengertian momentum sudut, rumus, sifat-sifatnya, hukum kekekalan momentum sudut, serta aplikasinya dalam kehidupan sehari-hari.
1. Pengertian Momentum Sudut
Momentum sudut didefinisikan sebagai ukuran dari seberapa sulitnya untuk mengubah keadaan rotasi suatu objek. Ini adalah besaran vektor yang bergantung pada dua faktor utama: momen inersia objek dan kecepatan sudutnya. Momentum sudut dapat dinyatakan dengan rumus:
![\[ L = I \cdot \omega \]](https://pengayaan.com/wp-content/uploads/2025/07/Hukum-Kekekalan-Momentum-Sudut.png "Rendered by QuickLaTeX.com")
Di mana:
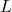= momentum sudut (dalam kilogram meter kuadrat per detik, kg·m²/s)
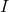= momen inersia (dalam kilogram meter kuadrat, kg·m²)
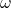= kecepatan sudut (dalam radian per detik, rad/s)
a. Momen Inersia
Momen inersia adalah ukuran distribusi massa suatu objek terhadap sumbu rotasi. Momen inersia tergantung pada bentuk dan ukuran objek serta sumbu rotasi yang dipilih. Untuk objek yang memiliki bentuk sederhana, momen inersia dapat dihitung dengan rumus tertentu. Misalnya, untuk silinder padat yang berputar di sekitar sumbu pusatnya, momen inersianya dapat dihitung dengan rumus:
![\[ I = \frac{1}{2} m r^2 \]](https://pengayaan.com/wp-content/uploads/2025/07/4_Hukum-Kekekalan-Momentum-Sudut.png "Rendered by QuickLaTeX.com")
Di mana:
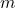= massa objek (dalam kilogram, kg)
= jari-jari objek (dalam meter, m)
2. Sifat-sifat Momentum Sudut
Momentum sudut memiliki beberapa sifat penting yang membedakannya dari momentum linier:
a. Vektor
Momentum sudut adalah besaran vektor, yang berarti ia memiliki arah dan besar. Arah momentum sudut ditentukan oleh aturan tangan kanan: jika jari-jari tangan kanan Anda mengikuti arah rotasi objek, maka ibu jari Anda akan menunjukkan arah momentum sudut.
b. Tergantung pada Sumbu Rotasi
Momentum sudut tergantung pada sumbu rotasi yang dipilih. Jika sumbu rotasi diubah, momen inersia dan, oleh karena itu, momentum sudut juga akan berubah. Ini penting dalam analisis gerakan rotasi, terutama ketika mempertimbangkan sistem yang memiliki lebih dari satu sumbu rotasi.
c. Kekekalan Momentum Sudut
Salah satu sifat paling penting dari momentum sudut adalah hukum kekekalan momentum sudut, yang menyatakan bahwa dalam sistem tertutup yang tidak mengalami gaya luar, total momentum sudut sistem akan tetap konstan. Ini mirip dengan hukum kekekalan momentum linier, tetapi berlaku untuk gerakan rotasi.
3. Hukum Kekekalan Momentum Sudut
Hukum kekekalan momentum sudut menyatakan bahwa jika tidak ada torsi eksternal yang bekerja pada sistem, maka total momentum sudut sistem akan tetap konstan. Ini dapat dinyatakan dalam bentuk matematis sebagai:
![\[ L_{\text{total, awal}} = L_{\text{total, akhir}} \]](https://pengayaan.com/wp-content/uploads/2025/07/7_Hukum-Kekekalan-Momentum-Sudut.png "Rendered by QuickLaTeX.com")
a. Contoh Penerapan
Salah satu contoh penerapan hukum kekekalan momentum sudut adalah pada sistem dua benda yang berputar. Misalkan dua orang yang berdiri di tepi sebuah piringan berputar. Jika salah satu orang bergerak ke arah pusat piringan, momen inersia sistem akan berkurang, dan untuk menjaga kekekalan momentum sudut, kecepatan sudut sistem harus meningkat. Ini menjelaskan mengapa piringan berputar akan berputar lebih cepat ketika seseorang bergerak ke dalam.
4. Aplikasi Momentum Sudut dalam Kehidupan Sehari-hari
Momentum sudut memiliki banyak aplikasi dalam kehidupan sehari-hari dan berbagai bidang ilmu. Beberapa contoh aplikasi momentum sudut meliputi:
a. Olahraga
Dalam olahraga, pemahaman tentang momentum sudut sangat penting. Misalnya, dalam senam, atlet menggunakan teknik rotasi untuk melakukan gerakan yang kompleks. Dengan mengubah posisi tubuh mereka, mereka dapat mengontrol kecepatan rotasi dan menyelesaikan gerakan dengan baik.
b. Kendaraan
Dalam desain kendaraan, momentum sudut diperhitungkan untuk meningkatkan stabilitas dan keamanan. Misalnya, roda kendaraan berputar dan memiliki momentum sudut yang membantu menjaga keseimbangan kendaraan saat bergerak.
c. Astronomi
Dalam astrofisika, momentum sudut digunakan untuk memahami gerakan planet, bintang, dan galaksi. Hukum kekekalan momentum sudut membantu ilmuwan menjelaskan bagaimana objek langit berinteraksi dan bergerak dalam ruang angkasa.
d. Teknologi dan Rekayasa
Momentum sudut juga digunakan dalam teknologi dan rekayasa, seperti dalam desain mesin, robotika, dan sistem transportasi. Pemahaman tentang momentum sudut membantu insinyur merancang sistem yang efisien dan aman.
5. Kesimpulan
Momentum sudut adalah konsep fundamental dalam fisika yang menggambarkan gerakan rotasi suatu objek. Dengan memahami momentum sudut, kita dapat menganalisis interaksi antara objek yang berputar dan memahami berbagai fenomena fisik yang terjadi di sekitar kita. Hukum kekekalan momentum sudut adalah prinsip dasar yang memungkinkan kita untuk menghitung perubahan momentum sudut dalam sistem tertutup. Aplikasi momentum sudut sangat luas, mencakup berbagai bidang, mulai dari olahraga hingga teknologi dan astrofisika. Dengan pemahaman yang baik tentang momentum sudut, kita dapat lebih menghargai dinamika gerakan dan interaksi di dunia sekitar kita.
