Pengertian Standar Deviasi
Standar deviasi adalah ukuran statistik yang digunakan untuk menentukan seberapa jauh data dalam suatu himpunan tersebar dari rata-ratanya. Semakin kecil standar deviasi, semakin dekat data terhadap nilai rata-rata, dan sebaliknya, semakin besar standar deviasi, semakin tersebar datanya.
Dalam analisis statistik, standar deviasi sering digunakan untuk mengukur variasi atau ketidakpastian dalam berbagai bidang seperti keuangan, sains, teknik, dan psikologi.
Fungsi Standar Deviasi
1. Mengukur Penyebaran Data
Standar deviasi membantu dalam memahami sejauh mana nilai-nilai data bervariasi dari rata-rata. Jika standar deviasi rendah, berarti mayoritas data mendekati rata-rata, sedangkan standar deviasi tinggi menunjukkan data yang lebih tersebar.
Contoh Ilustratif:
Misalkan ada dua kelas yang mengikuti ujian matematika:
- Kelas A: Nilai siswa adalah 80, 82, 78, 79, dan 81.
- Kelas B: Nilai siswa adalah 60, 90, 50, 95, dan 85.
Kedua kelas ini mungkin memiliki rata-rata nilai yang hampir sama, tetapi nilai di Kelas B lebih bervariasi dibandingkan dengan Kelas A. Standar deviasi Kelas B akan lebih tinggi, menunjukkan bahwa nilai-nilainya lebih tersebar dibandingkan dengan Kelas A.
2. Menentukan Risiko dalam Keuangan
Dalam dunia keuangan, standar deviasi digunakan untuk mengukur volatilitas aset atau investasi. Saham dengan standar deviasi tinggi memiliki fluktuasi harga yang lebih besar, sehingga lebih berisiko dibandingkan saham dengan standar deviasi rendah.
Contoh Ilustratif:
Misalkan ada dua saham:
- Saham X memiliki harga yang berubah dalam satu minggu: 100, 102, 99, 101, 100.
- Saham Y memiliki harga yang berubah dalam satu minggu: 100, 110, 90, 115, 85.
Meskipun rata-rata harga keduanya bisa sama, Saham Y memiliki perubahan harga yang lebih besar, sehingga memiliki standar deviasi yang lebih tinggi dan dianggap lebih berisiko.
3. Menguji Konsistensi dalam Produksi
Di industri manufaktur, standar deviasi digunakan untuk mengukur konsistensi dalam proses produksi. Produk dengan variasi ukuran atau berat yang kecil lebih diinginkan dibandingkan produk dengan variasi yang besar.
Contoh Ilustratif:
Misalkan sebuah pabrik memproduksi botol air dengan target volume 500 ml. Dari sampel yang diambil:
- Mesin A menghasilkan botol dengan volume: 499, 500, 501, 500, 499 ml.
- Mesin B menghasilkan botol dengan volume: 490, 510, 495, 505, 485 ml.
Mesin A memiliki standar deviasi lebih kecil dibandingkan Mesin B, yang berarti hasil produksinya lebih konsisten dan lebih dapat diandalkan.
4. Mengidentifikasi Data yang Tidak Normal
Dalam analisis data, standar deviasi sering digunakan untuk menemukan data yang menyimpang jauh dari rata-rata atau outlier.
Contoh Ilustratif:
Misalkan ada data tinggi badan siswa dalam suatu kelas dengan rata-rata 165 cm. Jika ada siswa yang memiliki tinggi 190 cm atau 140 cm, maka mereka bisa dianggap sebagai outlier karena berada jauh dari rata-rata.
Rumus Perhitungan Standar Deviasi
Standar deviasi dapat dihitung menggunakan rumus berikut:
![\[ \sigma = \sqrt{\frac{\sum (x_i - \bar{x})^2}{N}} \]](https://pengayaan.com/wp-content/uploads/2025/02/4-fungsi-standar-deviasi-dan-perhitungannya.png "Rendered by QuickLaTeX.com")
Di mana:
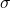= standar deviasi
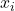= nilai individu dalam dataset
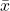= rata-rata (mean) dari dataset
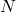= jumlah total data
Jika data merupakan sampel dari populasi yang lebih besar, rumusnya sedikit dimodifikasi menjadi:
![\[ s = \sqrt{\frac{\sum (x_i - \bar{x})^2}{N - 1}} \]](https://pengayaan.com/wp-content/uploads/2025/02/5_4-fungsi-standar-deviasi-dan-perhitungannya.png "Rendered by QuickLaTeX.com")
Contoh Perhitungan Standar Deviasi
Misalkan terdapat data nilai ujian lima siswa: 70, 75, 80, 85, 90
Langkah 1: Hitung Rata-Rata (Mean)
![\[ \bar{x} = \frac{70 + 75 + 80 + 85 + 90}{5} = 80 \]](https://pengayaan.com/wp-content/uploads/2025/02/6_4-fungsi-standar-deviasi-dan-perhitungannya.png "Rendered by QuickLaTeX.com")
Langkah 2: Hitung Selisih Tiap Nilai dari Mean, lalu Kuadratkan
| Nilai (xix_i) | Selisih dari Mean (xi−xˉx_i – \bar{x}) | Kuadrat Selisih |
|---|---|---|
| 70 | 70−80=−1070 – 80 = -10 | (−10)2=100(-10)^2 = 100 |
| 75 | 75−80=−575 – 80 = -5 | (−5)2=25(-5)^2 = 25 |
| 80 | 80−80=080 – 80 = 0 | 02=00^2 = 0 |
| 85 | 85−80=585 – 80 = 5 | 52=255^2 = 25 |
| 90 | 90−80=1090 – 80 = 10 | 102=10010^2 = 100 |
Langkah 3: Hitung Rata-Rata Kuadrat Selisih
![\[ \frac{100 + 25 + 0 + 25 + 100}{5} = \frac{250}{5} = 50 \]](https://pengayaan.com/wp-content/uploads/2025/02/7_4-fungsi-standar-deviasi-dan-perhitungannya.png "Rendered by QuickLaTeX.com")
Langkah 4: Ambil Akar Kuadrat dari Hasil
![\[ \sigma = \sqrt{50} = 7.07 \]](https://pengayaan.com/wp-content/uploads/2025/02/8_4-fungsi-standar-deviasi-dan-perhitungannya.png "Rendered by QuickLaTeX.com")
Jadi, standar deviasi dari data tersebut adalah 7.07.
Kesimpulan
Standar deviasi adalah alat statistik yang sangat berguna dalam berbagai bidang, mulai dari pendidikan, keuangan, hingga manufaktur. Dengan memahami standar deviasi, kita dapat mengukur penyebaran data, mengidentifikasi risiko, menilai konsistensi, dan mendeteksi outlier dalam suatu dataset.
Perhitungan standar deviasi mungkin tampak rumit pada awalnya, tetapi dengan latihan, konsep ini dapat diterapkan dengan mudah untuk menganalisis berbagai jenis data secara lebih akurat.