Tag: Standar Deviasi: Rumus dan Penerapan dalam Statistik

Standar deviasi adalah salah satu ukuran statistik yang digunakan untuk menggambarkan sebaran data dalam suatu kumpulan. Ukuran ini memberikan informasi tentang seberapa jauh nilai-nilai dalam dataset menyimpang dari rata-rata (mean) dataset tersebut. Dalam analisis data, standar deviasi sangat penting karena membantu kita memahami variabilitas dan konsistensi data. Dalam artikel ini, kita akan membahas secara mendetail tentang pengertian standar deviasi, rumus yang digunakan untuk menghitungnya, langkah-langkah perhitungan, serta penerapan standar deviasi dalam berbagai bidang, disertai dengan penjelasan ilustratif untuk setiap konsep.

Pengertian Standar Deviasi

Standar deviasi adalah ukuran yang menunjukkan seberapa besar variasi atau penyebaran nilai-nilai dalam suatu dataset. Semakin kecil nilai standar deviasi, semakin dekat nilai-nilai dalam dataset tersebut terhadap rata-rata, dan sebaliknya. Standar deviasi sering dilambangkan dengan huruf Yunani sigma (σ) untuk populasi dan huruf “s” untuk sampel.

Ilustrasi: Bayangkan standar deviasi sebagai “pengukur ketepatan.” Seperti pengukur yang menunjukkan seberapa tepat sebuah tembakan mengenai sasaran, standar deviasi menunjukkan seberapa dekat nilai-nilai dalam dataset terhadap rata-rata.

Rumus Standar Deviasi

Rumus untuk menghitung standar deviasi berbeda tergantung pada apakah kita menghitung untuk populasi atau sampel. Berikut adalah rumus untuk keduanya:

1. Standar Deviasi Populasi

Untuk menghitung standar deviasi populasi, rumusnya adalah:

    \[ \sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}} \]

Di mana:

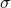  • \sigma = standar deviasi populasi
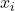  • x_i = setiap nilai dalam dataset
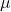  • \mu = rata-rata populasi
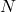  • N = jumlah total nilai dalam populasi

2. Standar Deviasi Sampel

Untuk menghitung standar deviasi sampel, rumusnya adalah:

    \[ s = \sqrt{\frac{\sum (x_i - \bar{x})^2}{n - 1}} \]

Di mana:

  • s = standar deviasi sampel
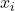  • x_i = setiap nilai dalam sampel
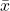  • \bar{x} = rata-rata sampel
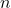  • n = jumlah total nilai dalam sampel

Ilustrasi: Bayangkan rumus standar deviasi sebagai “resep untuk menghitung variasi.” Seperti resep yang menunjukkan langkah-langkah untuk membuat kue, rumus ini memberikan langkah-langkah untuk menghitung seberapa jauh nilai-nilai dalam dataset menyimpang dari rata-rata.

Langkah-langkah Menghitung Standar Deviasi

Berikut adalah langkah-langkah untuk menghitung standar deviasi, baik untuk populasi maupun sampel:

1. Mengumpulkan Data

Kumpulkan data yang ingin dianalisis. Misalnya, kita memiliki dataset berikut: 5, 7, 8, 6, 10.

2. Menghitung Rata-rata

Hitung rata-rata (mean) dari dataset. Untuk dataset di atas:

    \[ \mu = \frac{5 + 7 + 8 + 6 + 10}{5} = \frac{36}{5} = 7.2 \]

3. Menghitung Selisih Kuadrat

Hitung selisih antara setiap nilai dan rata-rata, kemudian kuadratkan hasilnya:

  • (5 - 7.2)^2 = (-2.2)^2 = 4.84
  • (7 - 7.2)^2 = (-0.2)^2 = 0.04
  • (8 - 7.2)^2 = (0.8)^2 = 0.64
  • (6 - 7.2)^2 = (-1.2)^2 = 1.44
  • (10 - 7.2)^2 = (2.8)^2 = 7.84

4. Menjumlahkan Selisih Kuadrat

Jumlahkan semua hasil kuadrat:

    \[ \sum (x_i - \mu)^2 = 4.84 + 0.04 + 0.64 + 1.44 + 7.84 = 14.8 \]

5. Menghitung Varians

Untuk populasi, bagi jumlah selisih kuadrat dengan jumlah total nilai (N):

    \[ \sigma^2 = \frac{14.8}{5} = 2.96 \]

Untuk sampel, bagi jumlah selisih kuadrat dengan (n – 1):

    \[ s^2 = \frac{14.8}{4} = 3.7 \]

6. Menghitung Standar Deviasi

Ambil akar kuadrat dari varians untuk mendapatkan standar deviasi:

  • Untuk populasi:

    \[ \sigma = \sqrt{2.96} \approx 1.72 \]

  • Untuk sampel:

    \[ s = \sqrt{3.7} \approx 1.92 \]

Ilustrasi: Bayangkan langkah-langkah ini sebagai “proses pembuatan.” Seperti proses pembuatan kue yang melibatkan pengukuran dan pencampuran bahan, menghitung standar deviasi melibatkan langkah-langkah sistematis untuk mendapatkan hasil akhir.

Penerapan Standar Deviasi

Standar deviasi memiliki banyak penerapan dalam berbagai bidang, antara lain:

1. Statistik dan Analisis Data

Dalam statistik, standar deviasi digunakan untuk menggambarkan sebaran data. Ini membantu peneliti dan analis untuk memahami variabilitas dalam dataset dan membuat keputusan berdasarkan data tersebut.

Ilustrasi: Bayangkan standar deviasi dalam analisis data sebagai “kompas.” Seperti kompas yang membantu kita menemukan arah, standar deviasi membantu kita memahami sebaran data.

2. Keuangan

Dalam dunia keuangan, standar deviasi digunakan untuk mengukur risiko investasi. Semakin tinggi standar deviasi dari pengembalian investasi, semakin besar risiko yang terkait dengan investasi tersebut.

Ilustrasi: Bayangkan standar deviasi dalam keuangan sebagai “alat ukur risiko.” Seperti alat yang menunjukkan seberapa berisiko suatu investasi, standar deviasi membantu investor membuat keputusan yang lebih baik.

3. Kualitas dan Kontrol Proses

Dalam industri, standar deviasi digunakan untuk mengukur kualitas produk. Dengan memantau standar deviasi dari ukuran produk, perusahaan dapat memastikan bahwa produk yang dihasilkan memenuhi standar kualitas yang ditetapkan.

Ilustrasi: Bayangkan standar deviasi dalam kontrol kualitas sebagai “alat pengukur presisi.” Seperti alat yang memastikan bahwa produk sesuai dengan spesifikasi, standar deviasi membantu menjaga kualitas produk.

4. Pendidikan

Dalam pendidikan, standar deviasi digunakan untuk menganalisis hasil ujian dan penilaian. Ini membantu pendidik memahami sebaran nilai siswa dan mengidentifikasi area yang perlu diperbaiki.

Ilustrasi: Bayangkan standar deviasi dalam pendidikan sebagai “alat evaluasi.” Seperti alat yang membantu guru menilai kemajuan siswa, standar deviasi membantu dalam analisis hasil belajar.

Kesimpulan

Standar deviasi adalah ukuran penting dalam statistik yang menggambarkan sebaran data dan variabilitas nilai-nilai dalam suatu dataset. Dengan memahami pengertian, rumus, langkah-langkah perhitungan, dan penerapan standar deviasi, kita dapat lebih menghargai peranannya dalam analisis data dan pengambilan keputusan. Seperti pengukur ketepatan yang menunjukkan seberapa dekat nilai-nilai terhadap rata-rata, standar deviasi memberikan wawasan yang berharga dalam berbagai bidang, mulai dari statistik hingga keuangan dan pendidikan. Dengan pengetahuan ini, kita diharapkan dapat lebih memahami dan menerapkan konsep standar deviasi dalam kehidupan sehari-hari.

Fungsi Standar Deviasi dan Perhitungannya

Matematika

Fungsi Standar Deviasi dan Perhitungannya – Standar Deviasi yakni besar perbedaan dari nilai sampel terhadap rata-rata. Nilai sampel yakni sedikit dari jumlah keseluruhan objek yang diamati. Misalnya saja jika anda mencari tahu berapa jumlah alat musik yang dipunyai oleh mahasiswa jurusan music dari universitas X dan sampel yang anda ambil hanya 100 orang dari total […]