In geometry, angles are formed by the intersection of two rays (or line segments) that share a common endpoint, known as the vertex. Angles are fundamental in various fields, including mathematics, physics, engineering, and architecture. Understanding the relationships between different types of angles is crucial for solving geometric problems and proving theorems. This article aims to provide an exhaustive overview of adjacent and vertical angles, detailing their definitions, properties, relationships, and illustrative explanations for each concept.
1. Definition of Angles
Before delving into adjacent and vertical angles, it is essential to understand the basic definition of an angle. An angle is typically measured in degrees (°) or radians (rad) and can be classified based on its measure:
- Acute Angle: An angle that measures less than
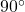 .
. - Right Angle: An angle that measures exactly
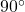 .
. - Obtuse Angle: An angle that measures more than
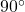 but less than
but less than 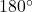 .
. - Straight Angle: An angle that measures exactly
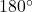 .
. - Reflex Angle: An angle that measures more than
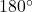 but less than
but less than 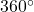 .
.
2. Adjacent Angles
2.1. Definition of Adjacent Angles
Adjacent angles are two angles that share a common vertex and a common side but do not overlap. In other words, they are next to each other and are formed by two rays that originate from the same vertex.
- Illustrative Explanation: Consider two angles,
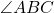 and
and 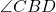 , where point
, where point 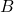 is the common vertex, and ray
is the common vertex, and ray 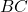 is the common side. The angles can be represented as follows:
is the common side. The angles can be represented as follows:
“` A | | B—–C | | D “`
In this diagram, ![]() and
and ![]() are adjacent angles because they share the vertex
are adjacent angles because they share the vertex ![]() and the side
and the side ![]() .
.
2.2. Properties of Adjacent Angles
1. Common Vertex and Side: As defined, adjacent angles share a common vertex and a common side.
2. Non-Overlapping: Adjacent angles do not overlap; they occupy different regions of the plane.
3. Sum of Angles: The sum of two adjacent angles can be any value, depending on their measures. For example, if ![]() and
and ![]() , then:
, then:
![]()
4. Linear Pair: If two adjacent angles form a straight line, they are called a linear pair, and their measures add up to ![]() .
.
- Illustrative Example: If
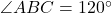 and
and 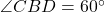 , they form a linear pair:
, they form a linear pair:
![]()
3. Vertical Angles
3.1. Definition of Vertical Angles
Vertical angles are the angles that are opposite each other when two lines intersect. When two lines cross, they form two pairs of vertical angles, which are always equal in measure.
- Illustrative Explanation: Consider two intersecting lines that create four angles, labeled as
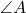 ,
, 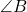 ,
, 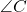 , and
, and 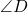 :
:
“` A | | B—–C | | D “`
In this diagram, ![]() and
and ![]() are vertical angles, as are
are vertical angles, as are ![]() and
and ![]() . The pairs of vertical angles are opposite each other at the intersection point.
. The pairs of vertical angles are opposite each other at the intersection point.
3.2. Properties of Vertical Angles
1. Equal Measures: Vertical angles are always equal. If ![]() , then
, then ![]() as well.
as well.
2. Formation: Vertical angles are formed by the intersection of two lines. Each pair of vertical angles consists of two angles that are opposite each other.
3. Non-Adjacent: Unlike adjacent angles, vertical angles are not next to each other; they are separated by the intersection of the lines.
4. Linear Pair Relationship: Each pair of vertical angles forms a linear pair with the adjacent angles. For example, if ![]() , then
, then ![]() and
and ![]() are supplementary angles.
are supplementary angles.
- Illustrative Example: If
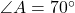 , then
, then 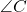 (the vertical angle) is also
(the vertical angle) is also 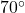 . If
. If 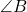 is adjacent to
is adjacent to 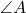 and measures
and measures 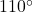 , then:
, then:
![]()
4. Relationships Between Adjacent and Vertical Angles
Adjacent and vertical angles are related through their geometric properties, particularly when lines intersect. Here are some key relationships:
4.1. Linear Pairs and Vertical Angles
When two lines intersect, they create adjacent angles that form linear pairs. The angles in each linear pair are supplementary, meaning their measures add up to ![]() . The vertical angles formed by the intersection are equal.
. The vertical angles formed by the intersection are equal.
- Illustrative Explanation: If two lines intersect and create angles
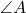 ,
, 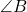 ,
, 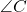 , and
, and 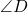 , then:
, then:
![]()
![]()
4.2. Applications in Geometry
Understanding adjacent and vertical angles is crucial in solving geometric problems, particularly in proofs and constructions. For example, when proving that two lines are parallel, one might use the properties of alternate interior angles, which are formed by a transversal intersecting two parallel lines.
- Illustrative Example: If two lines are cut by a transversal and the alternate interior angles are equal, then the lines are parallel. This relies on the relationships between adjacent and vertical angles.
5. Real-World Applications
The concepts of adjacent and vertical angles have practical applications in various fields:
5.1. Architecture and Engineering
In architecture and engineering, understanding angles is essential for designing structures. Adjacent and vertical angles help ensure that buildings are constructed with the correct angles for stability and aesthetics.
- Illustrative Explanation: When designing a roof, architects must consider the angles formed by the rafters. Ensuring that adjacent angles are complementary can help achieve the desired slope.
5.2. Navigation and Surveying
In navigation and surveying, angles are used to determine positions and distances. Vertical angles can help calculate heights and depths, while adjacent angles can assist in triangulation.
- Illustrative Explanation: Surveyors often use the concept of vertical angles to measure the height of a building or a tree by creating a right triangle with the ground.
5.3. Computer Graphics
In computer graphics, angles play a crucial role in rendering shapes and animations. Understanding adjacent and vertical angles helps in creating realistic models and animations.
- Illustrative Explanation: When animating a character, the angles between limbs must be calculated to ensure smooth and realistic movements.
Conclusion
In conclusion, adjacent and vertical angles are fundamental concepts in geometry that play a crucial role in understanding the relationships between angles formed by intersecting lines. Adjacent angles share a common vertex and side, while vertical angles are opposite each other and always equal in measure. The properties and relationships of these angles are essential for solving geometric problems and have practical applications in various fields, including architecture, engineering, navigation, and computer graphics. By mastering the concepts of adjacent and vertical angles, one can gain valuable insights into the geometric relationships that underpin many real-world scenarios. As we continue to explore the vast landscape of geometry, the knowledge of these angle types will remain a key component of our mathematical toolkit.