The concept of a line is fundamental in geometry and algebra, serving as a building block for more complex mathematical ideas. Understanding the general equation of a line is crucial for students and professionals in mathematics, engineering, physics, and various fields that involve analytical thinking. This article will provide a detailed exploration of the general equation of a line, including its definition, forms, properties, and illustrative explanations to enhance comprehension.
1. Definition of a Line
In mathematics, a line is defined as a straight one-dimensional figure that extends infinitely in both directions. It is characterized by having no thickness and is determined by at least two distinct points. The line can be represented in various forms, including slope-intercept form, point-slope form, and the general form.
2. General Equation of a Line
The general equation of a line in a two-dimensional Cartesian coordinate system can be expressed in the form:
![]()
Where:
 ,
, 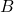 , and
, and 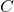 are constants.
are constants.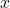 and
and  are the variables representing the coordinates of any point on the line.
are the variables representing the coordinates of any point on the line.
Illustrative Explanation:
To understand this equation, consider the following:
- If
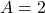 ,
, 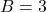 , and
, and 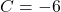 , the equation becomes:
, the equation becomes:
![]()
This equation represents a line in the Cartesian plane. Any point ![]() that satisfies this equation lies on the line.
that satisfies this equation lies on the line.
3. Forms of the Equation of a Line
While the general form is useful, there are other forms of the equation of a line that are often more convenient for specific applications.
A. Slope-Intercept Form
The slope-intercept form of a line is given by:
![]()
Where:
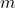 is the slope of the line.
is the slope of the line.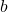 is the y-intercept, the point where the line crosses the y-axis.
is the y-intercept, the point where the line crosses the y-axis.
Illustrative Explanation:
For example, if the equation of a line is ![]() :
:
- The slope
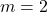 indicates that for every unit increase in
indicates that for every unit increase in 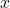 ,
,  increases by 2 units.
increases by 2 units. - The y-intercept
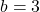 means the line crosses the y-axis at the point
means the line crosses the y-axis at the point 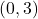 .
.
B. Point-Slope Form
The point-slope form of a line is expressed as:
![]()
Where:
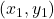 is a specific point on the line.
is a specific point on the line.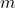 is the slope of the line.
is the slope of the line.
Illustrative Explanation:
If we have a line with a slope of 3 that passes through the point ![]() , the equation can be written as:
, the equation can be written as:
![]()
This form is particularly useful when you know a point on the line and the slope.
4. Finding the General Equation from Other Forms
To convert from slope-intercept or point-slope form to the general form, you can rearrange the equations.
A. From Slope-Intercept to General Form
Starting with the slope-intercept form:
![]()
Rearranging gives:
![]()
This can be expressed in the general form ![]() where
where ![]() ,
, ![]() , and
, and ![]() .
.
Illustrative Example:
For the equation ![]() :
:
1. Rearranging gives:
![]()
Thus, the general form is ![]() .
.
B. From Point-Slope to General Form
Starting with the point-slope form:
![]()
Expanding and rearranging gives:
![]()
Illustrative Example:
For the point-slope equation ![]() :
:
1. Expanding gives:
![]()
2. Rearranging gives:
![]()
Thus, the general form is ![]() .
.
5. Slope of a Line
The slope of a line is a measure of its steepness and direction. It is calculated as the ratio of the change in ![]() (vertical change) to the change in
(vertical change) to the change in ![]() (horizontal change) between two points on the line.
(horizontal change) between two points on the line.
Slope Formula:
If you have two points ![]() and
and ![]() , the slope
, the slope ![]() is given by:
is given by:
![]()
Illustrative Example:
Consider the points ![]() and
and ![]() :
:
1. Calculate the slope:
![]()
This means the line rises 2 units for every 1 unit it runs horizontally.
6. Intercepts of a Line
The intercepts of a line are the points where the line crosses the axes.
A. Y-Intercept
The y-intercept is found by setting ![]() in the equation of the line. The resulting value of
in the equation of the line. The resulting value of ![]() gives the point where the line crosses the y-axis.
gives the point where the line crosses the y-axis.
Illustrative Example:
For the equation ![]() :
:
1. Set ![]() :
:
![]()
Thus, the y-intercept is ![]() .
.
B. X-Intercept
The x-intercept is found by setting ![]() in the equation of the line. The resulting value of
in the equation of the line. The resulting value of ![]() gives the point where the line crosses the x-axis.
gives the point where the line crosses the x-axis.
Illustrative Example:
Continuing with the equation ![]() :
:
1. Set ![]() :
:
![]()
Thus, the x-intercept is ![]() .
.
7. Graphing a Line
Graphing a line involves plotting points that satisfy the line’s equation and drawing a straight line through these points.
Steps to Graph a Line:
1. Find the intercepts: Calculate the x-intercept and y-intercept.
2. Plot the intercepts: Mark the points on the Cartesian plane.
3. Use the slope: From the y-intercept, use the slope to find another point on the line.
4. Draw the line: Connect the points with a straight line, extending it in both directions.
Illustrative Example:
For the line represented by ![]() :
:
1. Intercepts: We found the intercepts to be ![]() and
and ![]() .
.
2. Plot: Mark these points on the graph.
3. Slope: The slope is ![]() , indicating a downward slope. From
, indicating a downward slope. From ![]() , move down 2 units and right 3 units to find another point
, move down 2 units and right 3 units to find another point ![]() .
.
4. Draw: Connect the points to form the line.
8. Applications of the General Equation of a Line
The general equation of a line has numerous applications across various fields:
A. Geometry
In geometry, lines are used to define shapes, angles, and other geometric properties. The general equation helps in determining relationships between different geometric figures.
B. Physics
In physics, linear equations can represent motion, forces, and other phenomena. For example, the relationship between distance and time in uniform motion can be modeled using a linear equation.
C. Economics
In economics, linear equations can model supply and demand, cost functions, and revenue. They help in analyzing trends and making predictions based on linear relationships.
D. Computer Graphics
In computer graphics, lines are essential for rendering shapes and images. The general equation of a line is used in algorithms for drawing lines on screens.
9. Conclusion
The general equation of a line is a fundamental concept in mathematics that provides a framework for understanding linear relationships in various contexts. By mastering the general form, slope, intercepts, and methods of graphing, individuals can effectively analyze and interpret linear equations in real-world applications.
Key Takeaways:
- The general equation of a line is expressed as
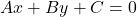 .
. - Different forms of the equation, such as slope-intercept and point-slope, are useful for specific applications.
- The slope indicates the steepness of the line, while intercepts provide key points for graphing.
- Understanding linear equations is essential for applications in geometry, physics, economics, and computer graphics.
By grasping these concepts, individuals can enhance their mathematical skills and apply them to solve problems in various fields, making informed decisions based on linear relationships.