Angular Displacement: A Comprehensive Exploration of Its Definition, Significance, and Applications

Angular displacement is a fundamental concept in physics and engineering that describes the change in the angle of an object as it rotates about a fixed point or axis. It is a vector quantity that provides essential information about the rotational motion of objects, such as wheels, gears, and celestial bodies. Understanding angular displacement is crucial for analyzing rotational dynamics, kinematics, and various applications in mechanics. This article aims to provide an exhaustive overview of angular displacement, detailing its definition, significance, calculation, and illustrative explanations of each concept.

Understanding Angular Displacement

1. Definition of Angular Displacement

Angular displacement is defined as the angle through which an object has rotated about a specific axis in a given time interval. It is typically measured in radians (rad), degrees (°), or revolutions (rev). The angular displacement ( $\Delta \theta$ ) can be expressed mathematically as:

$\Delta \theta = \theta_f - \theta_i$

Where:

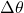$\Delta \theta$ is the angular displacement,
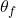$\theta_f$ is the final angle,
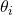$\theta_i$ is the initial angle.
Illustrative Explanation: Imagine a clock’s minute hand. If the minute hand moves from the 12 o’clock position (0 degrees) to the 3 o’clock position (90 degrees), the angular displacement is 90 degrees. This change in position represents how far the hand has rotated around the clock face.

2. Significance of Angular Displacement

Angular displacement is significant for several reasons:

a. Understanding Rotational Motion

Angular displacement provides a clear measure of how much an object has rotated, which is essential for analyzing rotational motion. It helps in understanding the dynamics of rotating systems, such as wheels, gears, and planets.

Illustrative Explanation: Consider a spinning top. The angular displacement tells us how far the top has spun from its starting position, allowing us to analyze its motion and stability.

b. Relationship with Linear Displacement

Angular displacement is related to linear displacement, especially in circular motion. The relationship can be expressed as:

$s = r \Delta \theta$

Where:

$s$ is the linear displacement,
$r$ is the radius of the circular path,
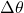$\Delta \theta$ is the angular displacement in radians.

This equation shows how the distance traveled along the circumference of a circle is directly related to the angle through which the object has rotated.

Illustrative Explanation: Imagine a bicycle wheel with a radius of 0.5 meters. If the wheel rotates through an angle of 90 degrees (or 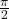$\frac{\pi}{2}$ radians), the linear displacement of a point on the edge of the wheel can be calculated using the formula. The point would have traveled a quarter of the circumference of the wheel.

c. Applications in Engineering and Physics

Angular displacement is crucial in various fields, including engineering, robotics, and physics. It is used to design and analyze mechanical systems, such as engines, turbines, and robotic arms, where precise control of rotational motion is required.

Illustrative Explanation: Think of a robotic arm that needs to pick up an object. The angular displacement helps engineers program the arm’s movements accurately, ensuring it reaches the desired position without overshooting or undershooting.

3. Calculation of Angular Displacement

Calculating angular displacement involves determining the initial and final angles of the rotating object. Here are some common scenarios:

a. Constant Angular Velocity

When an object rotates at a constant angular velocity ( $\omega$ ), the angular displacement can be calculated using the formula:

$\Delta \theta = \omega t$

Where:

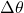$\Delta \theta$ is the angular displacement,
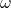$\omega$ is the angular velocity (in radians per second),
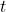$t$ is the time (in seconds).
Illustrative Explanation: Imagine a record player spinning at a constant speed of 33.3 revolutions per minute (RPM). If you observe the record for 10 seconds, you can calculate how far it has rotated in that time using the angular velocity.

b. Variable Angular Velocity

For objects with variable angular velocity, angular displacement can be calculated by integrating the angular velocity over time:

$\Delta \theta = \int_{t_i}^{t_f} \omega(t) \, dt$

Where:

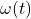$\omega(t)$ is the angular velocity as a function of time,
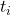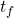$t_i$ and $t_f$ are the initial and final times.
Illustrative Explanation: Consider a Ferris wheel that accelerates as it starts moving. To find the total angular displacement during its motion, you would need to integrate the changing angular velocity over the time it takes to complete a full rotation.

4. Units of Angular Displacement

Angular displacement can be expressed in various units, including:

a. Radians

The radian is the standard unit of angular measurement in physics. One radian is defined as the angle subtended at the center of a circle by an arc equal in length to the radius of the circle. There are $2\pi$ radians in a full circle.

Illustrative Explanation: Imagine a circular pizza. If you take a slice of pizza with a crust length equal to the radius of the pizza, the angle at the center of the pizza is one radian.

b. Degrees

Degrees are another common unit for measuring angles, with one full circle equal to 360 degrees. To convert between radians and degrees, the following relationship can be used:

$\text{Degrees} = \text{Radians} \times \left( \frac{180}{\pi} \right)$

Illustrative Explanation: Think of a protractor used in geometry class. It measures angles in degrees, helping you visualize how far an object has rotated.

c. Revolutions

A revolution is a complete turn around a circle, equivalent to $2\pi$ radians or 360 degrees. This unit is often used in contexts involving circular motion, such as in machinery or sports.

Illustrative Explanation: Picture a merry-go-round. When it makes one complete turn, it has completed one revolution, which corresponds to a full angular displacement of 360 degrees or 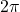$2\pi$ radians.

5. Applications of Angular Displacement

Angular displacement has numerous applications across various fields, including:

a. Mechanical Engineering

In mechanical engineering, angular displacement is used to analyze the motion of rotating machinery, such as engines, turbines, and gears. Understanding how components rotate relative to one another is essential for designing efficient systems.

Illustrative Explanation: Consider a car engine with rotating pistons. Engineers use angular displacement to ensure that the pistons move in sync, optimizing the engine’s performance.

b. Robotics

In robotics, angular displacement is crucial for programming the movements of robotic arms and joints. Precise control of angular displacement allows robots to perform tasks with accuracy and repeatability.

Illustrative Explanation: Imagine a robotic arm assembling a car. The arm must rotate its joints to specific angles to pick up and place components accurately. Angular displacement calculations ensure the arm moves correctly.

c. Astronomy

In astronomy, angular displacement is used to describe the motion of celestial bodies, such as planets and stars. Understanding their angular displacement helps astronomers predict their positions and movements over time.

Illustrative Explanation: Think of tracking the position of a planet in the night sky. Astronomers use angular displacement to calculate how far the planet has moved from its original position, allowing them to make accurate predictions.

d. Sports Science

In sports science, angular displacement is used to analyze the movements of athletes, such as runners, gymnasts, and divers. Understanding their rotational movements can help improve performance and reduce the risk of injury.

Illustrative Explanation: Consider a diver performing a somersault. Coaches analyze the diver’s angular displacement to ensure they complete the rotation correctly and enter the water smoothly.

Conclusion

In conclusion, angular displacement is a fundamental concept that describes the change in angle of an object as it rotates about a fixed point or axis. By exploring its definition, significance, calculation, units, and applications, we can appreciate the importance of angular displacement in various fields, including physics, engineering, robotics, astronomy, and sports science. Understanding this concept not only enhances our knowledge of rotational motion but also provides valuable insights into the dynamics of systems involving angular movement. As research and technology continue to advance, the study of angular displacement will remain essential for analyzing and optimizing the performance of rotating systems in our world.

Blog.Pengayaan.Com

Angular Displacement: A Comprehensive Exploration of Its Definition, Significance, and Applications

Understanding Angular Displacement

1. Definition of Angular Displacement

2. Significance of Angular Displacement

a. Understanding Rotational Motion

b. Relationship with Linear Displacement

c. Applications in Engineering and Physics

3. Calculation of Angular Displacement

a. Constant Angular Velocity

b. Variable Angular Velocity

4. Units of Angular Displacement

a. Radians

b. Degrees

c. Revolutions

5. Applications of Angular Displacement

a. Mechanical Engineering

b. Robotics

c. Astronomy

d. Sports Science

Conclusion

Leave a Reply Cancel reply