Applications of Trigonometry: A Comprehensive Exploration

Trigonometry, a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right triangles, has a wide array of applications across various fields. From engineering and physics to architecture and computer graphics, trigonometry plays a crucial role in solving real-world problems. This article aims to provide an exhaustive exploration of the applications of trigonometry, illustrating each concept with detailed explanations and examples to enhance understanding.

1. Engineering Applications

1.1 Structural Engineering

In structural engineering, trigonometry is essential for analyzing forces and designing structures. Engineers use trigonometric functions to calculate the angles and lengths of beams, trusses, and other structural components. For example, when designing a roof, engineers must determine the angle of the roof slope to ensure proper drainage and stability.

Illustrative Example: Consider a triangular truss used in a bridge. If the base of the triangle is 10 meters and the height is 6 meters, the angle at the base can be calculated using the tangent function:

$\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} = \frac{6}{10}$

To find the angle $\theta$ :

$\theta = \tan^{-1}\left(\frac{6}{10}\right) \approx 31^\circ$

This angle is crucial for determining the load distribution and stability of the truss.

1.2 Electrical Engineering

In electrical engineering, trigonometry is used to analyze alternating current (AC) circuits. Engineers use sine and cosine functions to represent voltage and current waveforms, which are periodic in nature. The phase difference between voltage and current can be calculated using trigonometric identities.

Illustrative Example: If the voltage in an AC circuit is represented as $V(t) = V_0 \sin(\omega t)$ and the current as $I(t) = I_0 \sin(\omega t + \phi)$ , where $\phi$ is the phase difference, the power factor can be calculated using the cosine of the phase angle:

$\text{Power Factor} = \cos(\phi)$

This calculation is essential for optimizing the efficiency of electrical systems.

2. Physics Applications

2.1 Mechanics

In mechanics, trigonometry is used to resolve forces into their components. When analyzing the motion of objects, especially in inclined planes or circular motion, trigonometric functions help in calculating the resultant forces acting on an object.

Illustrative Example: Consider a block sliding down an inclined plane with an angle $\theta$ . The gravitational force acting on the block can be resolved into two components: one parallel to the incline and one perpendicular to it.

The force parallel to the incline is given by:

$F_{\text{parallel}} = mg \sin(\theta)$

The force perpendicular to the incline is given by:

$F_{\text{perpendicular}} = mg \cos(\theta)$

Where $m$ is the mass of the block and $g$ is the acceleration due to gravity. These calculations are crucial for determining the acceleration of the block down the incline.

2.2 Wave Motion

Trigonometry is also fundamental in understanding wave motion, including sound and light waves. The properties of waves, such as amplitude, wavelength, and frequency, can be described using trigonometric functions.

Illustrative Example: The displacement of a wave can be represented as:

$y(x, t) = A \sin(kx - \omega t)$

Where:

$A$ is the amplitude,
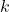$k$ is the wave number,
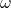$\omega$ is the angular frequency,
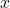$x$ is the position, and
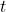$t$ is time.

This equation helps in analyzing the behavior of waves in different media.

3. Architecture and Construction

3.1 Design and Measurement

In architecture, trigonometry is used for designing buildings and structures. Architects use trigonometric principles to calculate heights, distances, and angles, ensuring that structures are both aesthetically pleasing and structurally sound.

Illustrative Example: When designing a building with a sloped roof, architects must calculate the height of the roof at a given distance from the base. If the distance from the base to the peak is 12 meters and the angle of elevation is 30 degrees, the height can be calculated using the sine function:

$\sin(30^\circ) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{h}{12}$

Solving for $h$ :

$h = 12 \sin(30^\circ) = 12 \times 0.5 = 6 \text{ meters}$

This calculation is vital for ensuring proper drainage and aesthetics.

3.2 Surveying

Trigonometry is extensively used in surveying to measure distances and angles on the Earth’s surface. Surveyors use triangulation methods to determine the location of points and the layout of land.

Illustrative Example: In a triangulation survey, if surveyors measure two angles from a known point to two other points, they can calculate the distance between those points using the Law of Sines:

$\frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)}$

Where $a$ , $b$ , and $c$ are the lengths of the sides opposite angles $A$ , $B$ , and $C$ , respectively. This method allows for accurate mapping and land division.

4. Computer Graphics

4.1 2D and 3D Modeling

In computer graphics, trigonometry is essential for rendering images and creating animations. Trigonometric functions are used to calculate angles, rotations, and transformations of objects in both 2D and 3D spaces.

Illustrative Example: When rotating a point $(x, y)$ around the origin by an angle $\theta$ , the new coordinates $(x', y')$ can be calculated using the rotation matrix:

$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$

This transformation is crucial for creating realistic animations and simulations.

4.2 Game Development

In game development, trigonometry is used to calculate trajectories, collisions, and movements of characters and objects. Understanding angles and distances is vital for creating immersive gaming experiences.

Illustrative Example: When a character jumps in a game, the trajectory can be modeled using projectile motion equations, which involve trigonometric functions to determine the maximum height and distance traveled based on the initial velocity and launch angle.

5. Astronomy

5.1 Celestial Navigation

Trigonometry is fundamental in astronomy for calculating distances between celestial bodies and determining their positions in the sky. Astronomers use trigonometric parallax to measure the distance to nearby stars.

Illustrative Example: If an observer measures the angle of a star from two different positions on Earth, the distance to the star can be calculated using the formula:

$d = \frac{1 \text{ AU}}{\tan(\theta)}$

Where $d$ is the distance to the star, $1 \text{ AU}$ is the average distance from the Earth to the Sun, and $\theta$ is the angle measured. This method is crucial for understanding the scale of the universe.

5.2 Orbital Mechanics

In orbital mechanics, trigonometry is used to calculate the orbits of planets and satellites. The positions and velocities of celestial objects can be determined using trigonometric functions.

Illustrative Example: The position of a satellite in orbit can be described using polar coordinates, where the radius $r$ and angle $\theta$ are related through trigonometric functions. The equations governing the motion of the satellite involve sine and cosine functions to describe its path.

Conclusion

In conclusion, trigonometry is an indispensable tool with a vast array of applications across multiple disciplines, including engineering, physics, architecture, computer graphics, and astronomy. Its ability to relate angles and distances makes it essential for solving practical problems and understanding complex systems. Through detailed exploration and illustrative examples, we can appreciate the profound impact of trigonometry on our daily lives and the advancement of technology and science. Whether it is designing a bridge, navigating the stars, or creating realistic animations, trigonometry continues to be a cornerstone of modern mathematics and its applications.

Blog.Pengayaan.Com