Area of a Sphere: A Comprehensive Overview

The sphere is one of the most fundamental shapes in geometry, representing a perfectly symmetrical three-dimensional object. It is defined as the set of all points in three-dimensional space that are equidistant from a fixed point known as the center. Understanding the area of a sphere is crucial in various fields, including mathematics, physics, engineering, and architecture. This article will explore the concept of the area of a sphere, the formula used to calculate it, the derivation of the formula, and illustrative explanations to enhance comprehension.

Definition of a Sphere

What is a Sphere?

A sphere is a three-dimensional object characterized by its round shape. It can be defined mathematically as follows:

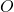Definition: A sphere is the set of all points in three-dimensional space that are at a constant distance $r$ (the radius) from a central point $O$ (the center).

Illustrative Explanation

To visualize a sphere, imagine a basketball. Every point on the surface of the basketball is the same distance from its center. This distance is the radius of the sphere. If you were to slice the basketball in half, you would see a circular cross-section, which is a two-dimensional representation of the sphere.

Formula for the Surface Area of a Sphere

Mathematical Formula

The surface area $A$ of a sphere can be calculated using the following formula:

$A = 4\pi r^2$

Where:

$A$ = surface area of the sphere
$r$ = radius of the sphere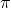
$\pi$ (pi) is a mathematical constant approximately equal to 3.14159.

Illustrative Explanation of the Formula

The formula $A = 4\pi r^2$ can be understood as follows:

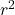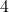The term $r^2$ represents the area of a circle with radius $r$ . Since a sphere can be thought of as an infinite number of circles stacked together, the factor of $4$ accounts for the total surface area of the sphere.
The constant 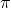$\pi$ is used because the area of a circle is calculated using 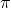$\pi$ as well.

Derivation of the Surface Area Formula

The derivation of the surface area formula for a sphere can be approached through calculus, specifically using the method of integration. Here, we will provide a simplified explanation of the derivation.

1. Concept of Slicing the Sphere

Imagine slicing the sphere into infinitesimally thin circular disks. Each disk has a radius that varies depending on its position along the height of the sphere.

2. Setting Up the Integral

To derive the surface area, we can use spherical coordinates. The surface area can be expressed as an integral over the sphere’s surface. The formula for the surface area $A$ can be derived by integrating the circumferences of these infinitesimally thin circles.

1. Circumference of a Circle: The circumference $C$ of a circle is given by:

$C = 2\pi r$

2. Differential Element: The differential surface area $dA$ of a thin band at a height $h$ on the sphere can be expressed as:

$dA = C \cdot dh = 2\pi r \cdot dh$

3. Integrating Over the Sphere: To find the total surface area, we integrate $dA$ over the height of the sphere from $-r$ to $r$ :

$A = \int_{-r}^{r} 2\pi r \, dh$

4. Evaluating the Integral: The integral evaluates to:

$A = 2\pi r \cdot (2r) = 4\pi r^2$

Conclusion of the Derivation

Thus, we arrive at the formula for the surface area of a sphere:

$A = 4\pi r^2$

Example Calculation

To illustrate the application of the formula, let’s calculate the surface area of a sphere with a radius of $5$ units.

Step-by-Step Calculation

1. Identify the Radius:

$r = 5 \text{ units}$

2. Substitute into the Formula:

$A = 4\pi (5^2)$

3. Calculate:

$A = 4\pi (25) = 100\pi$

4. Approximate Value:
Using $\pi \approx 3.14$ :

$A \approx 100 \times 3.14 = 314 \text{ square units}$

Illustrative Explanation of the Calculation

In this example, we found that the surface area of a sphere with a radius of $5$ units is approximately $314$ square units. This means that if you were to cover the entire surface of the sphere with a material, you would need about $314$ square units of that material.

Applications of the Surface Area of a Sphere

Understanding the surface area of a sphere has numerous practical applications across various fields:

1. Physics

In physics, the surface area of a sphere is important in calculations involving gravitational fields, heat transfer, and radiation. For example, the surface area of celestial bodies like planets and stars is crucial for understanding their physical properties.

2. Engineering

In engineering, the surface area of spheres is used in the design of tanks, pressure vessels, and other spherical structures. Knowing the surface area helps in determining the amount of material needed for construction and insulation.

3. Biology

In biology, the surface area-to-volume ratio of cells and organisms is significant for understanding metabolic rates and diffusion processes. Spherical cells, such as red blood cells, have a specific surface area that affects their function in transporting oxygen.

4. Astronomy

In astronomy, the surface area of celestial bodies is used to calculate their luminosity and energy output. Understanding the surface area helps astronomers estimate the amount of light emitted by stars and other astronomical objects.

5. Art and Design

In art and design, the concept of spheres and their surface areas is used in creating sculptures, ornaments, and architectural designs. Artists often use spheres to create visually appealing and balanced compositions.

Conclusion

The area of a sphere is a fundamental concept in geometry that has wide-ranging applications in various fields. The formula $A = 4\pi r^2$ provides a straightforward way to calculate the surface area of a sphere based on its radius. Through the derivation of the formula, we gain a deeper understanding of the relationship between the radius and the surface area. As we continue to explore the world of geometry and its applications, the concept of the area of a sphere will remain an essential tool for solving problems and understanding the properties of three-dimensional objects. Whether in physics, engineering, biology, or art, the sphere and its surface area play a vital role in our understanding of the world around us.

Blog.Pengayaan.Com