Area of an Isosceles Triangle: A Comprehensive Overview

An isosceles triangle is a special type of triangle characterized by having at least two sides of equal length. This unique property gives rise to specific geometric relationships and formulas, particularly when calculating the area of the triangle. Understanding how to find the area of an isosceles triangle is essential for students of geometry and has practical applications in various fields, including architecture, engineering, and design. This article will explore the definition of an isosceles triangle, the formula for calculating its area, the derivation of the formula, and illustrative explanations to enhance comprehension.

Definition of an Isosceles Triangle

What is an Isosceles Triangle?

An isosceles triangle is defined as a triangle that has at least two sides of equal length. The angles opposite these equal sides are also equal, which is a fundamental property of isosceles triangles.

Illustrative Explanation

To visualize an isosceles triangle, consider a triangle labeled $ABC$ where $AB = AC$ . In this case, sides $AB$ and $AC$ are equal, and the angle $A$ is the vertex angle, while angles $B$ and $C$ are the base angles.

“`
A
/ \
/ \
B—–C
“`

In this diagram, $AB$ and $AC$ are the equal sides, while $BC$ is the base of the triangle.

Formula for the Area of an Isosceles Triangle

Mathematical Formula

The area $A$ of an isosceles triangle can be calculated using the following formula:

$A = \frac{1}{2} \times b \times h$

Where:

$A$ = area of the triangle
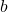$b$ = length of the base of the triangle
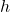$h$ = height of the triangle, which is the perpendicular distance from the vertex opposite the base to the base itself.

Illustrative Explanation of the Formula

The formula $A = \frac{1}{2} \times b \times h$ can be understood as follows:

The term 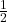$\frac{1}{2}$ accounts for the fact that we are calculating the area of a triangle, which is always half the area of a rectangle with the same base and height.
The base 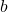$b$ represents the length of the side of the triangle that is not equal to the other two sides.
The height 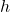$h$ is crucial because it measures how tall the triangle is from the base to the vertex opposite the base.

Derivation of the Area Formula

To derive the area formula for an isosceles triangle, we can use the properties of triangles and the Pythagorean theorem.

1. Drawing the Height

Consider an isosceles triangle $ABC$ with equal sides $AB$ and $AC$ and base $BC$ . To find the area, we first draw a height $AD$ from vertex $A$ to the midpoint $D$ of base $BC$ . This height divides the triangle into two right triangles, $ABD$ and $ACD$ .

“`
A
/|\
/ | \
B–D–C
“`

2. Identifying the Right Triangle

In triangle $ABD$ :

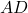$AD$ is the height $h$ .
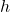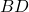$BD$ is half the length of the base 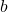$b$ , so $BD = \frac{b}{2}$ .
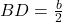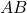$AB$ is the length of one of the equal sides.

3. Applying the Pythagorean Theorem

Using the Pythagorean theorem in triangle $ABD$ , we have:

$AB^2 = AD^2 + BD^2$

Substituting the known lengths:

$AB^2 = h^2 + \left(\frac{b}{2}\right)^2$

4. Solving for Height

Rearranging the equation to solve for height $h$ :

$h^2 = AB^2 - \left(\frac{b}{2}\right)^2$

Taking the square root gives us:

$h = \sqrt{AB^2 - \left(\frac{b}{2}\right)^2}$

5. Substituting Back into the Area Formula

Now, substituting $h$ back into the area formula:

$A = \frac{1}{2} \times b \times h = \frac{1}{2} \times b \times \sqrt{AB^2 - \left(\frac{b}{2}\right)^2}$

This formula allows us to calculate the area of an isosceles triangle when we know the lengths of the equal sides and the base.

Example Calculation

To illustrate the application of the area formula, let’s calculate the area of an isosceles triangle with a base of $8$ units and equal sides of $5$ units.

Step-by-Step Calculation

1. Identify the Base and Equal Sides:
– Base $b = 8$ units
– Equal sides $AB = AC = 5$ units

2. Calculate the Height:
Using the derived formula for height:

$h = \sqrt{AB^2 - \left(\frac{b}{2}\right)^2}$

First, calculate $\frac{b}{2}$ :

$\frac{b}{2} = \frac{8}{2} = 4 \text{ units}$

Now substitute into the height formula:

$h = \sqrt{5^2 - 4^2} = \sqrt{25 - 16} = \sqrt{9} = 3 \text{ units}$

3. Calculate the Area:
Now substitute $b$ and $h$ into the area formula:

$A = \frac{1}{2} \times 8 \times 3 = 12 \text{ square units}$

Illustrative Explanation of the Calculation

In this example, we found that the area of the isosceles triangle with a base of $8$ units and equal sides of $5$ units is $12$ square units. This means that if you were to cover the entire surface of the triangle with a material, you would need $12$ square units of that material.

Applications of the Area of an Isosceles Triangle

Understanding the area of an isosceles triangle has numerous practical applications across various fields:

1. Architecture

In architecture, isosceles triangles are often used in the design of roofs, trusses, and other structural elements. Calculating the area helps architects determine the amount of materials needed for construction.

2. Engineering

Engineers use isosceles triangles in various applications, including the design of bridges and support structures. Knowing the area is essential for analyzing load distribution and stability.

3. Art and Design

In art and design, isosceles triangles are frequently used in creating visually appealing compositions. Understanding the area helps artists and designers balance their work and create harmonious designs.

4. Geography

In geography, isosceles triangles can represent landforms, such as mountains or hills. Calculating the area can help in understanding the size and scale of these features.

5. Computer Graphics

In computer graphics, isosceles triangles are used in rendering shapes and models. Understanding the area is important for texture mapping and shading calculations.

Conclusion

The area of an isosceles triangle is a fundamental concept in geometry that has wide-ranging applications in various fields. The formula $A = \frac{1}{2} \times b \times h$ provides a straightforward way to calculate the area based on the base and height of the triangle. Through the derivation of the formula and the example calculation, we gain a deeper understanding of the relationship between the dimensions of the triangle and its area. As we continue to explore the world of geometry and its applications, the concept of the area of an isosceles triangle will remain an essential tool for solving problems and understanding the properties of triangles. Whether in architecture, engineering, art, or computer graphics, the isosceles triangle plays a vital role in our understanding of shapes and their applications in the real world.

Blog.Pengayaan.Com