In mathematics, functions are essential constructs that describe relationships between sets. Among the various types of functions, bijective functions hold a special significance due to their unique properties. Understanding bijective functions is crucial for various fields, including algebra, calculus, and computer science. This article will provide a detailed exploration of bijective functions, including their definition, properties, examples, and illustrative explanations to enhance understanding.
1. Definition of Bijective Functions
A bijective function is a function that is both injective (one-to-one) and surjective (onto). This means that every element in the domain of the function maps to a unique element in the codomain, and every element in the codomain is the image of some element in the domain. In simpler terms, a bijective function establishes a perfect pairing between the elements of the domain and the codomain.
Mathematical Notation:
If ![]() is a bijective function, then:
is a bijective function, then:
- Injective: For every
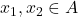 , if
, if 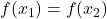 , then
, then 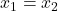 .
. - Surjective: For every
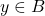 , there exists at least one
, there exists at least one 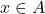 such that
such that 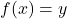 .
.
Illustrative Explanation:
Consider a function ![]() that assigns students to their unique student IDs. If each student has a distinct ID and every ID corresponds to exactly one student, then the function is bijective. For example:
that assigns students to their unique student IDs. If each student has a distinct ID and every ID corresponds to exactly one student, then the function is bijective. For example:
- Let
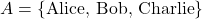
- Let
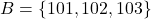
The function ![]() can be defined as:
can be defined as:
In this case, ![]() is bijective because each student has a unique ID, and every ID corresponds to a unique student.
is bijective because each student has a unique ID, and every ID corresponds to a unique student.
2. Properties of Bijective Functions
Bijective functions possess several important properties that make them particularly useful in mathematics:
A. Inverse Function
One of the most significant properties of bijective functions is that they have an inverse function. If ![]() is bijective, then there exists an inverse function
is bijective, then there exists an inverse function ![]() such that:
such that:
![]()
![]()
Illustrative Explanation:
Using the previous example of students and IDs, the inverse function ![]() would map IDs back to students:
would map IDs back to students:
This demonstrates that the inverse function effectively reverses the mapping established by the original function.
B. Cardinality Preservation
Bijective functions preserve the cardinality (size) of sets. If ![]() is bijective, then the number of elements in set
is bijective, then the number of elements in set ![]() is equal to the number of elements in set
is equal to the number of elements in set ![]() :
:
![]()
Illustrative Explanation:
In our example, if there are three students in set ![]() and three unique IDs in set
and three unique IDs in set ![]() , the cardinality is preserved:
, the cardinality is preserved:
![]()
This property is crucial in various mathematical contexts, such as counting and combinatorics.
C. Composition of Functions
The composition of two bijective functions is also bijective. If ![]() and
and ![]() are both bijective, then the composite function
are both bijective, then the composite function ![]() is bijective.
is bijective.
Illustrative Explanation:
Let’s consider two bijective functions:
Since both functions are bijective, every element in ![]() maps to a unique element in
maps to a unique element in ![]() , and every element in
, and every element in ![]() maps to a unique element in
maps to a unique element in ![]() . Therefore, the composite function
. Therefore, the composite function ![]() will also establish a unique mapping from
will also establish a unique mapping from ![]() to
to ![]() .
.
3. Examples of Bijective Functions
A. Example 1: Linear Function
Consider the linear function:
![]()
Domain: All real numbers ![]()
Codomain: All real numbers ![]()
Injective: To show that ![]() is injective, assume
is injective, assume ![]() :
:
![]()
Thus, ![]() is injective.
is injective.
Surjective: For any ![]() , we can find
, we can find ![]() such that
such that ![]() :
:
![]()
Since we can find an ![]() for every
for every ![]() ,
, ![]() is surjective.
is surjective.
Since ![]() is both injective and surjective, it is bijective.
is both injective and surjective, it is bijective.
B. Example 2: Exponential Function
Consider the function:
![]()
Domain: All real numbers ![]()
Codomain: All positive real numbers ![]()
Injective: Assume ![]() :
:
![]()
Thus, ![]() is injective.
is injective.
Surjective: For any ![]() , we can find
, we can find ![]() such that
such that ![]() :
:
![]()
Since we can find an ![]() for every
for every ![]() ,
, ![]() is surjective.
is surjective.
Thus, ![]() is bijective.
is bijective.
C. Example 3: Quadratic Function
Consider the function:
![]()
Domain: All real numbers ![]()
Codomain: All non-negative real numbers ![]()
Injective: This function is not injective because ![]() for any
for any ![]() . For example,
. For example, ![]() and
and ![]() .
.
Surjective: The function is surjective onto the codomain ![]() because for every
because for every ![]() , there exists an
, there exists an ![]() such that
such that ![]() (specifically,
(specifically, ![]() or
or ![]() ).
).
Since ![]() is not injective, it is not bijective.
is not injective, it is not bijective.
4. Visual Representation of Bijective Functions
To further clarify the concept of bijective functions, consider the following visual representation:
- Injective: A function is injective if no horizontal line intersects the graph more than once. This indicates that each output corresponds to exactly one input.
- Surjective: A function is surjective if every horizontal line intersects the graph at least once. This indicates that every element in the codomain is covered by the function.
Illustrative Explanation:
For the function ![]() :
:
- The graph is a straight line with a slope of 2, which means it is both injective and surjective, thus bijective.
For the function ![]() :
:
- The graph is a parabola that opens upwards. A horizontal line at
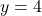 intersects the graph at two points (
intersects the graph at two points (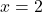 and
and 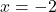 ), indicating that the function is not injective.
), indicating that the function is not injective.
5. Applications of Bijective Functions
Bijective functions have numerous applications across various fields:
A. Mathematics
In mathematics, bijective functions are used to establish isomorphisms between algebraic structures, such as groups, rings, and vector spaces. An isomorphism is a bijective function that preserves the structure of the sets involved.
B. Computer Science
In computer science, bijective functions are essential in cryptography, data encoding, and hashing. They ensure that data can be uniquely mapped and retrieved without loss of information.
C. Statistics
In statistics, bijective functions are used in transformations to ensure that data maintains its properties while being manipulated. For example, a bijective transformation can be used to normalize data.
6. Conclusion
In summary, bijective functions are a vital concept in mathematics that establish a one-to-one correspondence between the elements of the domain and codomain. Understanding the definition, properties, and examples of bijective functions is essential for analyzing and manipulating mathematical relationships. Through illustrative explanations and examples, we can appreciate the significance of bijective functions in mathematical reasoning and their practical applications in various fields, including algebra, calculus, and computer science. As we continue to explore the world of mathematics, the concept of bijective functions will remain central to our understanding of how functions interact, leading to deeper insights and enhanced problem-solving skills. This understanding not only enriches our mathematical knowledge but also empowers us to apply these concepts in diverse disciplines, fostering innovative solutions and insights.