BODMAS Rule: A Comprehensive Overview

The BODMAS rule is a fundamental principle in mathematics that dictates the order of operations when solving mathematical expressions. Understanding this rule is essential for students, educators, and anyone involved in mathematical calculations, as it ensures that expressions are evaluated correctly and consistently. This article will explore the components of the BODMAS rule, its significance, and illustrative examples to enhance comprehension.

What is BODMAS?

Definition

BODMAS is an acronym that stands for:

B: Brackets
O: Orders (i.e., powers and roots, such as squares and square roots)
D: Division
M: Multiplication
A: Addition
S: Subtraction

The BODMAS rule specifies the order in which operations should be performed in a mathematical expression to obtain the correct result.

Illustrative Explanation: Imagine you are baking a cake with multiple steps. Just as you must follow a specific order—mixing ingredients, baking, and then decorating—the BODMAS rule provides a structured approach to solving mathematical problems, ensuring that each operation is performed in the correct sequence.

Importance of BODMAS

The BODMAS rule is crucial for several reasons:

1. Clarity: It provides a clear guideline for solving mathematical expressions, reducing ambiguity and confusion.

2. Consistency: Following the BODMAS rule ensures that everyone arrives at the same answer when solving a given expression, promoting consistency in mathematical communication.

3. Foundation for Advanced Mathematics: A solid understanding of the BODMAS rule is essential for tackling more complex mathematical concepts, such as algebra, calculus, and beyond.

Components of BODMAS

Let’s delve deeper into each component of the BODMAS rule to understand its significance and application.

1. Brackets (B)

Brackets indicate that the operations enclosed within them should be performed first. There are different types of brackets, including parentheses $( )$ , square brackets $[ ]$ , and curly braces $\{ \}$ .

Illustrative Explanation: Think of brackets as a priority signal in a busy intersection. Just as traffic lights direct vehicles to stop or go, brackets indicate which operations should be prioritized in a mathematical expression.

Example: In the expression $3 \times (2 + 5)$ , the operation inside the brackets, $2 + 5$ , must be performed first, resulting in:

$3 \times (2 + 5) = 3 \times 7 = 21$

2. Orders (O)

Orders refer to powers and roots, such as squares and square roots. This operation is performed after brackets but before division, multiplication, addition, and subtraction.

Illustrative Explanation: Consider orders as the special tasks that require extra attention. Just as a chef might need to prepare a special sauce before cooking the main dish, orders must be calculated before moving on to other operations.

Example: In the expression $2 + 3^2$ , the exponentiation $3^2$ must be calculated first:

$2 + 3^2 = 2 + 9 = 11$

3. Division (D) and Multiplication (M)

Division and multiplication are of equal precedence and are performed from left to right. This means that if both operations appear in the same expression, you should perform them in the order they appear.

Illustrative Explanation: Imagine you are at a restaurant where you need to divide a bill among friends and also multiply the cost of items. You handle these tasks in the order they come up, just like you would in a mathematical expression.

Example: In the expression $8 \div 2 \times 4$ , you perform the division first:

$8 \div 2 = 4 \quad \text{then} \quad 4 \times 4 = 16$

4. Addition (A) and Subtraction (S)

Like division and multiplication, addition and subtraction also have equal precedence and are performed from left to right.

Illustrative Explanation: Think of addition and subtraction as two friends who always work together. You can’t prioritize one over the other; instead, you handle them in the order they appear, just like you would when organizing tasks.

Example: In the expression $10 - 3 + 2$ , you perform the operations from left to right:

$10 - 3 = 7 \quad \text{then} \quad 7 + 2 = 9$

Putting BODMAS into Practice

To illustrate the application of the BODMAS rule, let’s solve a more complex expression step by step.

Example Expression: 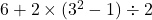$6 + 2 \times (3^2 - 1) \div 2$

1. Brackets: Solve the expression inside the brackets first:

$3^2 - 1 = 9 - 1 = 8$

Now the expression becomes:

$6 + 2 \times 8 \div 2$

2. Orders: There are no further orders to calculate.

3. Division and Multiplication: Perform multiplication and division from left to right:
– First, calculate $2 \times 8$ :

$2 \times 8 = 16$

– Then, divide by $2$ :

$16 \div 2 = 8$

Now the expression simplifies to:

$6 + 8$

4. Addition: Finally, perform the addition:

$6 + 8 = 14$

Thus, the final result of the expression $6 + 2 \times (3^2 - 1) \div 2$ is $14$ .

Common Mistakes to Avoid

Understanding the BODMAS rule is crucial, but it’s also important to be aware of common mistakes that can lead to incorrect results:

1. Ignoring Brackets: Failing to perform operations inside brackets first can lead to significant errors. Always prioritize brackets.

2. Misunderstanding Orders: Forgetting to calculate powers before moving on to multiplication or division can alter the outcome.

3. Left to Right Confusion: When division and multiplication (or addition and subtraction) appear together, remember to perform them from left to right, rather than prioritizing one over the other.

Illustrative Explanation: Think of these mistakes as shortcuts that lead you off the main road. Just as taking a wrong turn can lead to getting lost, skipping steps in the BODMAS rule can lead to incorrect answers.

Conclusion

The BODMAS rule is an essential guideline for solving mathematical expressions accurately and efficiently. By understanding the order of operations—brackets, orders, division, multiplication, addition, and subtraction—students and professionals can ensure that they arrive at the correct results. Mastering the BODMAS rule not only enhances mathematical skills but also lays the foundation for more advanced concepts in mathematics. Whether you are solving simple arithmetic problems or tackling complex equations, the BODMAS rule will serve as a reliable compass, guiding you through the intricacies of mathematical operations.

Blog.Pengayaan.Com