Centripetal Acceleration: Definition, Calculation, and Applications

Centripetal acceleration is a fundamental concept in physics that describes the acceleration experienced by an object moving in a circular path. This acceleration is directed towards the center of the circle around which the object is moving, and it plays a crucial role in understanding the dynamics of circular motion. Whether it’s a car turning around a curve, a planet orbiting a star, or a roller coaster navigating a loop, centripetal acceleration is a key factor in the analysis of these motions. This article aims to provide an exhaustive overview of centripetal acceleration, detailing its definition, calculation, factors affecting it, and applications, along with illustrative explanations of each concept.

Understanding Centripetal Acceleration

1. Definition of Centripetal Acceleration

Centripetal acceleration ( $a_c$ ) is defined as the acceleration that acts on an object moving in a circular path, directed towards the center of the circle. It is responsible for changing the direction of the object’s velocity, allowing it to maintain circular motion. The formula for calculating centripetal acceleration is given by:

$a_c = \frac{v^2}{r}$

Where:

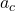$a_c$ is the centripetal acceleration,
$v$ is the linear velocity of the object,
$r$ is the radius of the circular path.
Illustrative Explanation: Imagine a child swinging a ball on a string in a circular motion. The ball moves around in a circle, and the string pulls it towards the center. This inward pull is what keeps the ball moving in a circle, and the acceleration towards the center is the centripetal acceleration. If the child were to let go of the string, the ball would fly off in a straight line, demonstrating that the centripetal acceleration is necessary to keep it moving in a circular path.

2. Direction of Centripetal Acceleration

Centripetal acceleration always points towards the center of the circular path, regardless of the direction of the object’s motion. This inward direction is crucial because it is what allows the object to continuously change its direction while maintaining a constant speed.

Illustrative Explanation: Consider a car driving around a circular track. Even if the car maintains a constant speed, it is constantly changing direction. The centripetal acceleration acts inward, towards the center of the track, ensuring that the car follows the curved path instead of moving off in a straight line.

Calculation of Centripetal Acceleration

3. Calculating Centripetal Acceleration

To calculate centripetal acceleration, you can use the formula mentioned earlier. Let’s break down the components involved in the calculation:

a. Linear Velocity (v)

Linear velocity is the speed of the object moving along the circular path. It can be calculated using the formula:

$v = \frac{d}{t}$

Where:

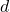$d$ is the distance traveled along the circular path,
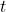$t$ is the time taken to travel that distance.
Illustrative Explanation: If a car travels around a circular track with a circumference of 100 meters in 10 seconds, its linear velocity would be $v = \frac{100 \, \text{m}}{10 \, \text{s}} = 10 \, \text{m/s}$ .

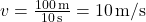b. Radius of the Circular Path (r)

The radius is the distance from the center of the circle to the path of the object. It is a crucial factor in determining the amount of centripetal acceleration experienced by the object.

Illustrative Explanation: If the car is driving around a track with a radius of 25 meters, this radius will be used in the centripetal acceleration calculation.

c. Putting It All Together

Using the values of linear velocity and radius, you can calculate the centripetal acceleration. For example, if the car has a linear velocity of 10 m/s and is traveling around a circular track with a radius of 25 m, the centripetal acceleration would be:

$a_c = \frac{v^2}{r} = \frac{(10 \, \text{m/s})^2}{25 \, \text{m}} = \frac{100 \, \text{m}^2/\text{s}^2}{25 \, \text{m}} = 4 \, \text{m/s}^2$

Illustrative Explanation: This means that the car experiences an acceleration of 4 m/s² directed towards the center of the circular track, which is necessary to keep it moving in that circular path.

Factors Affecting Centripetal Acceleration

4. Speed of the Object

The speed of the object directly affects the centripetal acceleration. As the speed increases, the centripetal acceleration increases as well, since it is proportional to the square of the velocity ( $v^2$ ).

Illustrative Explanation: Imagine a roller coaster car going around a loop. If the car speeds up as it approaches the loop, the centripetal acceleration increases, allowing it to stay on the track. If it slows down too much, it may not have enough centripetal acceleration to complete the loop.

5. Radius of the Circular Path

The radius of the circular path inversely affects the centripetal acceleration. A smaller radius results in greater centripetal acceleration for a given speed, while a larger radius results in lower centripetal acceleration.

Illustrative Explanation: Consider two cars on circular tracks: one with a small radius and one with a large radius. If both cars are traveling at the same speed, the car on the smaller track will experience a greater centripetal acceleration because it has to turn more sharply to maintain its circular path.

Applications of Centripetal Acceleration

6. Automobile Design

Centripetal acceleration is a critical factor in automobile design, particularly in the development of tires and suspension systems. Engineers must ensure that vehicles can handle the centripetal forces experienced during turns without losing traction.

Illustrative Explanation: Think of a car taking a sharp turn. The tires must grip the road effectively to provide the necessary centripetal acceleration. If the tires are not designed to handle the forces, the car may skid or roll over.

7. Astronomy and Planetary Motion

Centripetal acceleration is essential in understanding the motion of celestial bodies. Planets orbiting stars experience centripetal acceleration due to the gravitational pull of the star, which keeps them in their orbits.

Illustrative Explanation: Imagine the Earth orbiting the Sun. The gravitational force between the Earth and the Sun acts as the centripetal force, providing the necessary centripetal acceleration to keep the Earth in its elliptical orbit.

8. Amusement Park Rides

Centripetal acceleration is a key consideration in the design of amusement park rides, especially those that involve loops and sharp turns. Engineers must calculate the required centripetal acceleration to ensure the safety and enjoyment of riders.

Illustrative Explanation: Consider a roller coaster that goes through a loop. The design must ensure that the centripetal acceleration is sufficient to keep riders securely in their seats as they navigate the loop, preventing them from falling out.

9. Sports and Athletics

In sports, athletes often experience centripetal acceleration when running around curves or during activities that involve circular motion, such as gymnastics or figure skating. Understanding this acceleration can help improve performance and reduce the risk of injury.

Illustrative Explanation: Think of a sprinter running around a track. As they approach a curve, they must lean into the turn to maintain their balance and provide the necessary centripetal acceleration to stay on the track.

Conclusion

In conclusion, centripetal acceleration is a fundamental concept in physics that describes the acceleration experienced by an object moving in a circular path. By understanding its definition, calculation, factors affecting it, and various applications, we can appreciate the significance of centripetal acceleration in everyday life and various fields of study. From automobile design to planetary motion and amusement park rides, centripetal acceleration plays a crucial role in ensuring safety, performance, and functionality. As we continue to explore the principles of motion, the study of centripetal acceleration will remain essential for understanding the dynamics of circular motion and its implications in the physical world.

Blog.Pengayaan.Com