Understanding the Circumcenter of a Triangle: A Comprehensive Guide

The circumcenter of a triangle is a fundamental concept in geometry that plays a crucial role in various mathematical applications. It is one of the triangle’s points of concurrency, which are points where certain lines intersect. The circumcenter is particularly significant because it is the center of the circumcircle, the circle that passes through all three vertices of the triangle. This article will provide a detailed exploration of the circumcenter, including its definition, properties, methods of construction, and illustrative examples to enhance understanding.

Definition of the Circumcenter

The circumcenter of a triangle is defined as the point where the perpendicular bisectors of the sides of the triangle intersect. This point is equidistant from all three vertices of the triangle, making it the center of the circumcircle. The circumcircle is the unique circle that can be drawn around the triangle, touching all three vertices.

Properties of the Circumcenter

1. Equidistance from Vertices: The circumcenter is equidistant from all three vertices of the triangle. If $O$ is the circumcenter and $A$ , $B$ , and $C$ are the vertices of the triangle, then:

$OA = OB = OC$

2. Location Based on Triangle Type:
– Acute Triangle: The circumcenter lies inside the triangle.
– Right Triangle: The circumcenter is located at the midpoint of the hypotenuse.
– Obtuse Triangle: The circumcenter lies outside the triangle.

3. Circumradius: The radius of the circumcircle, denoted as $R$ , is the distance from the circumcenter to any of the triangle’s vertices. This radius can be calculated using the formula:

$R = \frac{abc}{4A}$

Where $a$ , $b$ , and $c$ are the lengths of the sides of the triangle, and $A$ is the area of the triangle.

Construction of the Circumcenter

To construct the circumcenter of a triangle, follow these steps:

Step 1: Draw the Triangle

Begin by drawing triangle $ABC$ with vertices $A$ , $B$ , and $C$ .

Step 2: Find the Midpoints

Calculate the midpoints of at least two sides of the triangle. For example, find the midpoints $M_{AB}$ of side $AB$ and $M_{AC}$ of side $AC$ .

The midpoint 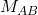$M_{AB}$ can be found using the formula:

$M_{AB} = \left(\frac{x_A + x_B}{2}, \frac{y_A + y_B}{2}\right)$

Similarly, calculate $M_{AC}$ .

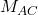Step 3: Draw Perpendicular Bisectors

Next, draw the perpendicular bisectors of the segments $AB$ and $AC$ . To do this:

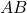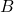Use a compass to draw arcs above and below the line segment $AB$ from points $A$ and $B$ . The intersection points of these arcs will help you draw the perpendicular bisector.
Repeat this process for segment $AC$ .

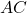Step 4: Locate the Circumcenter

The point where the two perpendicular bisectors intersect is the circumcenter $O$ of triangle $ABC$ .

Example of Finding the Circumcenter

Let’s consider a specific example to illustrate the process of finding the circumcenter.

Example Triangle: Triangle $ABC$ with vertices at $A(0, 0)$ , $B(4, 0)$ , and $C(2, 3)$ .

Step 1: Find Midpoints

Midpoint 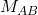$M_{AB}$ of side $AB$ :

$M_{AB} = \left(\frac{0 + 4}{2}, \frac{0 + 0}{2}\right) = (2, 0)$

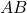Midpoint 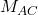$M_{AC}$ of side $AC$ :

$M_{AC} = \left(\frac{0 + 2}{2}, \frac{0 + 3}{2}\right) = (1, 1.5)$

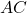Step 2: Draw Perpendicular Bisectors

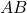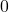The slope of line segment $AB$ is $0$ (horizontal line), so the perpendicular bisector will be a vertical line through 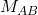$M_{AB}$ at $x = 2$ .
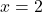The slope of line segment 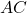$AC$ can be calculated as:

$\text{slope of } AC = \frac{3 - 0}{2 - 0} = \frac{3}{2}$

The slope of the perpendicular bisector will be the negative reciprocal:

$\text{slope of perpendicular bisector} = -\frac{2}{3}$

Using point-slope form to find the equation of the perpendicular bisector through $M_{AC}(1, 1.5)$ :

$y - 1.5 = -\frac{2}{3}(x - 1)$

Simplifying this gives:

$y = -\frac{2}{3}x + \frac{2}{3} + 1.5 = -\frac{2}{3}x + \frac{5}{3}$

Step 3: Find Intersection of Perpendicular Bisectors

Now, we need to find the intersection of the lines $x = 2$ and $y = -\frac{2}{3}(2) + \frac{5}{3}$ :

$y = -\frac{4}{3} + \frac{5}{3} = \frac{1}{3}$

Thus, the circumcenter $O$ is located at:

$O(2, \frac{1}{3})$

Circumradius Calculation

To find the circumradius $R$ of triangle $ABC$ , we can use the formula:

$R = \frac{abc}{4A}$

Step 1: Calculate Side Lengths

Using the distance formula, we find the lengths of the sides:

Length $AB$ :

$AB = \sqrt{(4 - 0)^2 + (0 - 0)^2} = 4$

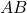Length $AC$ :

$AC = \sqrt{(2 - 0)^2 + (3 - 0)^2} = \sqrt{4 + 9} = \sqrt{13}$

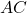Length $BC$ :

$BC = \sqrt{(2 - 4)^2 + (3 - 0)^2} = \sqrt{4 + 9} = \sqrt{13}$

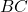Step 2: Calculate Area $A$

Using the formula for the area of a triangle with vertices at $(x_1, y_1)$ , $(x_2, y_2)$ , and $(x_3, y_3)$ :

$A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|$

Substituting the coordinates of points $A(0, 0)$ , $B(4, 0)$ , and $C(2, 3)$ :

$A = \frac{1}{2} \left| 0(0 - 3) + 4(3 - 0) + 2(0 - 0) \right| = \frac{1}{2} \left| 0 + 12 + 0 \right| = \frac{12}{2} = 6$

Step 3: Calculate Circumradius $R$

Now substituting the values into the circumradius formula:

$R = \frac{4 \cdot \sqrt{13} \cdot \sqrt{13}}{4 \cdot 6} = \frac{4 \cdot 13}{24} = \frac{52}{24} = \frac{13}{6} \approx 2.17$

Applications of the Circumcenter

The circumcenter has several important applications in various fields:

1. Geometric Constructions: The circumcenter is used in geometric constructions, such as creating circumcircles and determining the properties of triangles.

2. Navigation and Surveying: In navigation, the circumcenter can help determine the optimal location for facilities or resources based on distances to various points.

3. Computer Graphics: In computer graphics, the circumcenter is used in algorithms for rendering shapes and determining visibility.

4. Robotics: In robotics, the circumcenter can be used in path planning and obstacle avoidance, ensuring that robots maintain optimal distances from obstacles.

Conclusion

In conclusion, the circumcenter of a triangle is a vital concept in geometry that serves as the center of the circumcircle, equidistant from all three vertices of the triangle. Understanding the properties, construction methods, and applications of the circumcenter is essential for solving various geometric problems and has practical implications in fields such as architecture, engineering, and computer science. Through detailed explanations, proofs, and illustrative examples, we can appreciate the significance of the circumcenter in both theoretical and practical contexts. Whether constructing geometric figures or applying these principles in real-world scenarios, the circumcenter remains a cornerstone of geometric understanding.

Blog.Pengayaan.Com