Co-prime numbers, also known as relatively prime numbers, are a fundamental concept in number theory and mathematics. They play a significant role in various mathematical applications, including fractions, ratios, and modular arithmetic. This article aims to provide a detailed exploration of co-prime numbers, including their definition, properties, methods of identification, applications, and illustrative explanations to enhance understanding.
1. Definition of Co-Prime Numbers
Two integers 
and 
are said to be co-prime (or relatively prime) if the only positive integer that divides both of them is 
. In other words, the greatest common divisor (GCD) of and is . Co-prime numbers do not need to be prime themselves; they simply must not share any common factors other than .
Illustrative Explanation
To visualize co-prime numbers, consider the integers 
and 
. The factors of are 
, and the factors of are 
. The only common factor between them is , which means that and are co-prime.
Conversely, consider the integers 
and 
. The factors of are 
, and the factors of are 
. Since they share common factors 
, the GCD is 
, indicating that and are not co-prime.
2. Properties of Co-Prime Numbers
Understanding the properties of co-prime numbers is essential for their application in various mathematical contexts. Here are some key properties:
2.1. Co-Prime Pairs
Any two prime numbers are co-prime. For example, the prime numbers 
and 
are co-prime because they do not share any factors other than .
2.2. Co-Prime with One
The number is co-prime with every integer. This is because the only factor of is itself, and it does not share any other common factors with any integer.
2.3. Co-Prime Sets
A set of numbers can be co-prime as a whole. For example, the numbers , 
, and 
are co-prime to each other because no two numbers in the set share any common factors other than .
2.4. Multiplication of Co-Prime Numbers
If two numbers are co-prime, their product is also co-prime with any number that is co-prime to either of the two numbers. For example, if and are co-prime, and 
is co-prime to , then 
is co-prime to .
3. Methods of Identifying Co-Prime Numbers
Identifying co-prime numbers can be done through various methods, including:
3.1. Prime Factorization
One effective method to determine if two numbers are co-prime is to perform prime factorization. By breaking down each number into its prime factors, you can check for any common factors.
Example Calculation
Consider the numbers 
and :
- Prime Factorization of :
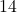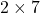
- Prime Factorization of :
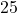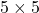
Since there are no common prime factors, and are co-prime.
3.2. Euclidean Algorithm
The Euclidean algorithm is a systematic method for finding the GCD of two numbers. If the GCD is , the numbers are co-prime.
Example Calculation
To determine if 
and 
are co-prime using the Euclidean algorithm:
1. Divide by : 
2. Divide by 
: 
3. Divide by : 
4. Divide by : 
5. Divide by : 
Since the last non-zero remainder is , the GCD of and is , indicating that they are co-prime.
4. Applications of Co-Prime Numbers
Co-prime numbers have numerous applications across various fields:
4.1. Cryptography
In cryptography, particularly in public key cryptography, co-prime numbers are essential for generating keys. The RSA algorithm, for example, relies on the properties of co-prime numbers to encrypt and decrypt messages securely.
4.2. Simplifying Fractions
Co-prime numbers are used to simplify fractions. A fraction is in its simplest form when the numerator and denominator are co-prime. For instance, the fraction 
is already in its simplest form because and are co-prime.
4.3. Number Theory
In number theory, co-prime numbers are used to study the properties of integers, including divisibility, modular arithmetic, and the distribution of prime numbers.
4.4. Combinatorics
In combinatorics, co-prime numbers are used in problems involving arrangements and selections, particularly when considering sets of numbers that do not share common factors.
5. Conclusion
Co-prime numbers are a fundamental concept in mathematics that plays a vital role in various applications, including cryptography, number theory, and data simplification. By understanding the definition, properties, methods of identification, and applications of co-prime numbers, one can appreciate their importance in both theoretical and practical contexts.
In summary, co-prime numbers are integers that share no common factors other than . Whether through prime factorization or the Euclidean algorithm, identifying co-prime numbers enhances problem-solving skills and provides valuable insights into the relationships between integers. By mastering the concept of co-prime numbers, individuals can deepen their understanding of mathematics and its applications in the real world.