Elastic collisions are a fundamental concept in physics that describe interactions between objects where both momentum and kinetic energy are conserved. These types of collisions are essential for understanding various physical phenomena, from the behavior of gas molecules to the dynamics of sports and engineering applications. This article will provide a detailed exploration of elastic collisions, including their definition, characteristics, mathematical formulations, examples, and illustrative explanations to enhance understanding.
1. Definition of Elastic Collision
An elastic collision is defined as a collision between two or more objects in which both momentum and kinetic energy are conserved. This means that the total momentum and the total kinetic energy of the system before the collision are equal to the total momentum and total kinetic energy after the collision.
Mathematical Representation
For two objects involved in an elastic collision, the conservation of momentum can be expressed as:
![]()
Where:
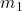 and
and 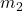 are the masses of the two objects,
are the masses of the two objects,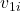 and
and 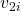 are the initial velocities of the objects before the collision,
are the initial velocities of the objects before the collision,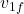 and
and 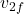 are the final velocities of the objects after the collision.
are the final velocities of the objects after the collision.
The conservation of kinetic energy can be expressed as:
![]()
Illustrative Explanation: Imagine two billiard balls colliding on a pool table. Before the collision, each ball has a certain speed and direction. After they collide, they bounce off each other, and if the collision is elastic, they will continue to move with speeds that conserve both their total momentum and total kinetic energy.
2. Characteristics of Elastic Collisions
A. Conservation of Momentum
In an elastic collision, the total momentum of the system remains constant. This principle is derived from Newton’s third law of motion, which states that for every action, there is an equal and opposite reaction.
Illustrative Explanation: Consider two ice skaters pushing off each other on a frictionless ice surface. If one skater is heavier than the other, they will move apart with different speeds, but the total momentum of the system (the combined momentum of both skaters) will remain unchanged.
B. Conservation of Kinetic Energy
In addition to momentum, the total kinetic energy of the system is also conserved in elastic collisions. This is a key distinguishing feature of elastic collisions compared to inelastic collisions, where kinetic energy is not conserved.
Illustrative Explanation: Think of a perfectly elastic rubber ball bouncing off the ground. When the ball hits the ground, it compresses and then expands back to its original shape, converting potential energy back into kinetic energy, allowing it to bounce back to nearly the same height from which it fell.
C. No Permanent Deformation
In elastic collisions, the objects involved do not undergo any permanent deformation. They return to their original shapes after the collision, which is a characteristic of elastic materials.
Illustrative Explanation: Imagine two perfectly elastic balls colliding. After the collision, they will not have any dents or changes in shape; they will look and behave as they did before the collision.
3. Types of Elastic Collisions
Elastic collisions can be categorized based on the relative motion of the colliding objects:
A. Head-On Elastic Collisions
In a head-on elastic collision, the objects collide directly along a straight line. This type of collision is often analyzed in one dimension.
Illustrative Explanation: Picture two cars moving towards each other on a straight road. When they collide head-on, they will bounce off each other, and their speeds can be calculated using the conservation laws.
B. Oblique Elastic Collisions
In oblique elastic collisions, the objects collide at an angle. This type of collision requires consideration of both the x and y components of momentum.
Illustrative Explanation: Imagine two soccer players kicking a ball at an angle. When the ball is struck, it will change direction and speed based on the angle of impact, and both players will exert forces on each other, conserving momentum in two dimensions.
4. Mathematical Analysis of Elastic Collisions
To analyze elastic collisions mathematically, we can derive the final velocities of two colliding objects using the conservation laws. For two objects with masses ![]() and
and ![]() and initial velocities
and initial velocities ![]() and
and ![]() , the final velocities after an elastic collision can be calculated using the following formulas:
, the final velocities after an elastic collision can be calculated using the following formulas:
![]()
![]()
Illustrative Explanation: Suppose a small ball (mass ![]() ) moving at
) moving at ![]() collides elastically with a larger ball (mass
collides elastically with a larger ball (mass ![]() ) at rest (
) at rest (![]() ). Using the formulas, we can calculate the final velocities of both balls after the collision.
). Using the formulas, we can calculate the final velocities of both balls after the collision.
1. For the small ball:
![]()
(The negative sign indicates that the small ball reverses direction.)
2. For the larger ball:
![]()
After the collision, the small ball moves backward at 1 m/s, while the larger ball moves forward at 2 m/s.
5. Examples of Elastic Collisions
A. Billiard Balls
A classic example of elastic collisions occurs in billiards. When one billiard ball strikes another, both momentum and kinetic energy are conserved. The balls will bounce off each other, and their final velocities can be calculated using the principles discussed.
Illustrative Explanation: Imagine a player strikes the cue ball, which then collides with the eight ball. The cue ball transfers some of its momentum and energy to the eight ball, causing it to move while the cue ball slows down. The interaction can be analyzed using the conservation equations.
B. Gas Molecules
In the kinetic theory of gases, elastic collisions are assumed between gas molecules. When gas molecules collide, they exchange momentum and kinetic energy without any loss, which is essential for understanding gas behavior.
Illustrative Explanation: Picture a container filled with gas molecules moving randomly. When two molecules collide, they bounce off each other, conserving momentum and energy. This behavior is crucial for explaining gas pressure and temperature.
C. Sports Applications
In sports like tennis or squash, the elastic collision between the ball and the racket or wall is vital for understanding how the ball rebounds. The speed and angle at which the ball leaves the racket can be analyzed using the principles of elastic collisions.
Illustrative Explanation: When a tennis player hits the ball, the racket exerts a force on the ball, causing it to bounce off with a certain speed and direction. The collision is elastic, and the player can use this knowledge to improve their technique and shot placement.
6. Limitations of Elastic Collisions
While elastic collisions are an important idealization, real-world collisions often involve some degree of inelasticity, where kinetic energy is not conserved due to factors such as:
A. Deformation
In many collisions, objects may deform, leading to energy loss in the form of heat or sound. For example, a car crash typically results in crumpled metal and energy dissipation.
Illustrative Explanation: Consider two cars colliding in a parking lot. The impact may cause dents and damage, indicating that not all kinetic energy is conserved as the cars crumple upon impact.
B. Friction and Air Resistance
Friction between surfaces and air resistance can also lead to energy loss during collisions, making them less than perfectly elastic.
Illustrative Explanation: If a basketball is dropped, it will not bounce back to its original height due to air resistance and energy loss during the impact with the ground. This illustrates how real-world conditions can affect the idealized concept of elastic collisions.
7. Conclusion
In summary, elastic collisions are a fundamental concept in physics characterized by the conservation of both momentum and kinetic energy. They play a crucial role in various applications, from understanding molecular behavior in gases to analyzing sports dynamics. By grasping the principles of elastic collisions, we can better appreciate the interactions between objects and the underlying physical laws governing motion. While real-world collisions may deviate from the idealized elastic model, the concepts remain essential for analyzing and predicting the behavior of colliding bodies in a wide range of contexts. Understanding elastic collisions not only enhances our knowledge of physics but also provides valuable insights into everyday phenomena and technological applications.