Equivalent Fractions: A Comprehensive Overview

Fractions are a fundamental concept in mathematics, representing parts of a whole. Among the various types of fractions, equivalent fractions play a crucial role in understanding the relationships between different fractions. Equivalent fractions are fractions that represent the same value or proportion, even though they may have different numerators and denominators. This article will explore the definition of equivalent fractions, how to identify and create them, their properties, and their applications in everyday life, complete with illustrative explanations to enhance comprehension.

What is a Fraction?

Definition of a Fraction

A fraction consists of two parts: the numerator and the denominator. The numerator represents the number of parts we have, while the denominator represents the total number of equal parts into which the whole is divided. A fraction is typically written in the form:

$\frac{a}{b}$

where:

$a$ is the numerator.
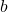$b$ is the denominator.
Illustrative Explanation: Imagine a pizza divided into 8 equal slices. If you eat 3 slices, you can represent this as the fraction 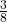$\frac{3}{8}$ , where 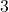$3$ is the number of slices you have eaten (numerator) and 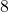$8$ is the total number of slices (denominator).

What are Equivalent Fractions?

Definition of Equivalent Fractions

Equivalent fractions are fractions that represent the same value or proportion, even though they may have different numerators and denominators. For example, the fractions $\frac{1}{2}$ and $\frac{2}{4}$ are equivalent because they both represent the same portion of a whole.

Illustrative Explanation: If you have a chocolate bar divided into 2 equal pieces and you eat 1 piece, you have consumed 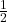$\frac{1}{2}$ of the bar. If the same chocolate bar is divided into 4 equal pieces and you eat 2 pieces, you have consumed 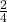$\frac{2}{4}$ of the bar. Both fractions represent the same amount of chocolate eaten, making them equivalent.

Visual Representation of Equivalent Fractions

Visual aids can help illustrate the concept of equivalent fractions. Consider the following examples:

1. Example 1: Fraction Circles
– A circle divided into 2 equal parts, with 1 shaded, represents $\frac{1}{2}$ .
– A circle divided into 4 equal parts, with 2 shaded, represents $\frac{2}{4}$ .
– Both circles show the same shaded area, demonstrating that $\frac{1}{2}$ and $\frac{2}{4}$ are equivalent.

2. Example 2: Fraction Bars
– A bar divided into 3 equal sections, with 1 section shaded, represents $\frac{1}{3}$ .
– A bar divided into 6 equal sections, with 2 sections shaded, represents $\frac{2}{6}$ .
– The shaded areas are the same, indicating that $\frac{1}{3}$ and $\frac{2}{6}$ are equivalent.

How to Identify Equivalent Fractions

Method 1: Cross-Multiplication

One effective way to determine if two fractions are equivalent is to use cross-multiplication. For two fractions $\frac{a}{b}$ and $\frac{c}{d}$ , they are equivalent if:

$a \times d = b \times c$

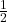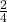Illustrative Explanation: To check if $\frac{1}{2}$ and $\frac{2}{4}$ are equivalent:

– Cross-multiply: $1 \times 4 = 4$ and $2 \times 2 = 4$ .
– Since both products are equal, $\frac{1}{2}$ and $\frac{2}{4}$ are equivalent fractions.

Method 2: Simplifying Fractions

Another way to identify equivalent fractions is to simplify a fraction to its lowest terms. If two fractions simplify to the same fraction, they are equivalent.

Illustrative Explanation: Consider the fraction $\frac{6}{8}$ :

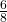– To simplify, divide both the numerator and denominator by their greatest common divisor (GCD), which is $2$ :

$\frac{6 \div 2}{8 \div 2} = \frac{3}{4}$

– If you compare $\frac{6}{8}$ with $\frac{3}{4}$ , you can see they are equivalent.

How to Create Equivalent Fractions

Creating equivalent fractions is straightforward and involves multiplying or dividing the numerator and denominator by the same non-zero number.

Method 1: Multiplying by a Whole Number

To create equivalent fractions, you can multiply both the numerator and denominator of a fraction by the same whole number.

Illustrative Explanation: Starting with the fraction $\frac{1}{3}$ :

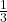– Multiply both the numerator and denominator by $2$ :

$\frac{1 \times 2}{3 \times 2} = \frac{2}{6}$

– Thus, $\frac{1}{3}$ and $\frac{2}{6}$ are equivalent fractions.

Method 2: Dividing by a Whole Number

You can also create equivalent fractions by dividing both the numerator and denominator by the same non-zero number, provided that the result remains a whole number.

Illustrative Explanation: Starting with the fraction $\frac{4}{8}$ :

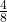– Divide both the numerator and denominator by $4$ :

$\frac{4 \div 4}{8 \div 4} = \frac{1}{2}$

– Therefore, $\frac{4}{8}$ and $\frac{1}{2}$ are equivalent fractions.

Properties of Equivalent Fractions

Understanding the properties of equivalent fractions can help reinforce the concept:

1. Same Value: Equivalent fractions represent the same value or proportion, even if they have different numerators and denominators.

2. Infinite Equivalents: For any given fraction, there are infinitely many equivalent fractions. For example, $\frac{1}{2}$ can be expressed as $\frac{2}{4}, \frac{3}{6}, \frac{10}{20},$ and so on.

3. Simplification: Any fraction can be simplified to its lowest terms, which is an equivalent fraction. For example, $\frac{12}{16}$ simplifies to $\frac{3}{4}$ .

Applications of Equivalent Fractions

Equivalent fractions have numerous applications in everyday life, including:

1. Cooking and Baking

In cooking, recipes often require measurements that can be expressed in different fractions. Understanding equivalent fractions allows cooks to adjust recipes based on available ingredients.

Illustrative Explanation: If a recipe calls for 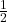$\frac{1}{2}$ cup of sugar, but you only have a 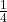$\frac{1}{4}$ cup measuring cup, you can use two 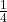$\frac{1}{4}$ cups to achieve the same amount:

$\frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2}$

2. Shopping and Discounts

When shopping, understanding equivalent fractions can help consumers calculate discounts and compare prices.

Illustrative Explanation: If a store offers a 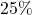$25\%$ discount on an item priced at $40, you can express the discount as 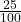$\frac{25}{100}$ of the price. This means you can calculate the discount amount:

$\frac{25}{100} \times 40 = 10$

Thus, the discount is $10, and the final price is $30.

3. Measurement and Construction

In construction and carpentry, measurements are often expressed as fractions. Understanding equivalent fractions helps ensure accuracy in cutting materials.

Illustrative Explanation: If a carpenter needs a piece of wood that is 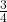$\frac{3}{4}$ of a foot long, they can also express this as 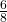$\frac{6}{8}$ of a foot or 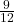$\frac{9}{12}$ of a foot, depending on the tools and measurements available.

Conclusion

Equivalent fractions are a fundamental concept in mathematics that helps us understand the relationships between different fractions. By exploring the definition of equivalent fractions, how to identify and create them, their properties, and their applications in everyday life, we gain valuable skills that enhance our ability to work with fractions effectively. Whether in cooking, shopping, or construction, the concept of equivalent fractions plays a vital role in ensuring accuracy and clarity in our calculations. As we continue to encounter fractions in various contexts, a solid understanding of equivalent fractions will empower us to navigate the world of mathematics with confidence and precision.

Blog.Pengayaan.Com