Understanding Even Numbers: A Comprehensive Guide

Even numbers are a fundamental concept in mathematics, playing a crucial role in various branches of number theory, arithmetic, and algebra. They are one of the simplest and most easily recognizable categories of integers. This article will provide a detailed exploration of even numbers, including their definition, properties, classifications, operations involving even numbers, and illustrative examples to enhance understanding.

Definition of Even Numbers

An even number is defined as any integer that is exactly divisible by 2. In mathematical terms, an integer $n$ is considered even if there exists an integer $k$ such that:

$n = 2k$

Where:

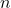$n$ is the even number.
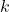$k$ is any integer (which can be positive, negative, or zero).

Illustrative Example: The numbers 0, 2, 4, 6, 8, 10, and so on are all even numbers because they can be expressed as $2 \times k$ for some integer $k$ . For instance:

$0 = 2 \times 0$
$2 = 2 \times 1$
$4 = 2 \times 2$
$6 = 2 \times 3$

Properties of Even Numbers

Even numbers possess several important properties that distinguish them from odd numbers (which are not divisible by 2). Here are some key properties of even numbers:

1. Divisibility: As mentioned, even numbers are divisible by 2 without leaving a remainder. This property is the defining characteristic of even numbers.

2. Sum of Even Numbers: The sum of any two even numbers is always even. This can be expressed mathematically:
– If $a$ and $b$ are even numbers, then $a + b$ is even.

Illustrative Example:
– $2 + 4 = 6$ (even)
– $10 + 14 = 24$ (even)

3. Difference of Even Numbers: The difference between any two even numbers is also even.
– If $a$ and $b$ are even numbers, then $a - b$ is even.

Illustrative Example:
– $8 - 4 = 4$ (even)
– $20 - 10 = 10$ (even)

4. Product of Even Numbers: The product of any two even numbers is always even.
– If $a$ and $b$ are even numbers, then $a \times b$ is even.

Illustrative Example:
– $2 \times 4 = 8$ (even)
– $6 \times 10 = 60$ (even)

5. Even and Odd Numbers: The sum or difference of an even number and an odd number is always odd.
– If $a$ is even and $b$ is odd, then $a + b$ is odd.

Illustrative Example:
– $2 + 3 = 5$ (odd)
– $4 - 1 = 3$ (odd)

6. Zero: Zero (0) is considered an even number because it can be expressed as $2 \times 0$ . It is the only integer that is neither positive nor negative.

Classification of Even Numbers

Even numbers can be classified into different categories based on their properties:

1. Positive Even Numbers: These are even numbers greater than zero. Examples include 2, 4, 6, 8, 10, etc.

2. Negative Even Numbers: These are even numbers less than zero. Examples include -2, -4, -6, -8, -10, etc.

3. Zero: As mentioned earlier, zero is an even number and serves as a unique case in the classification of integers.

Operations Involving Even Numbers

Understanding how even numbers interact with other numbers through various operations is essential in mathematics. Here are some operations involving even numbers:

1. Addition:
– Adding two even numbers results in an even number.
– Adding an even number and an odd number results in an odd number.

Illustrative Example:
– $4 + 6 = 10$ (even)
– $4 + 3 = 7$ (odd)

2. Subtraction:
– Subtracting two even numbers results in an even number.
– Subtracting an odd number from an even number results in an odd number.

Illustrative Example:
– $10 - 4 = 6$ (even)
– $6 - 3 = 3$ (odd)

3. Multiplication:
– Multiplying two even numbers results in an even number.
– Multiplying an even number by an odd number results in an even number.

Illustrative Example:
– $2 \times 4 = 8$ (even)
– $2 \times 3 = 6$ (even)

4. Division:
– Dividing an even number by 2 results in an integer (which can be even or odd).
– Dividing an even number by an odd number can result in either an even or an odd number, depending on the specific numbers involved.

Illustrative Example:
– $8 \div 2 = 4$ (even)
– $8 \div 4 = 2$ (even)
– $8 \div 3 = 2.67$ (not an integer)

Applications of Even Numbers

Even numbers have various applications in mathematics and real life:

1. Mathematical Patterns: Even numbers are often used in mathematical patterns and sequences, such as arithmetic sequences where the common difference is an even number.

2. Computer Science: In computer programming, even numbers are frequently used in algorithms, particularly in sorting and searching algorithms, where parity (even or odd) can determine the flow of logic.

3. Game Theory: In game theory, even numbers can be used to create balanced scenarios, such as in games where players take turns or where resources are distributed evenly.

4. Statistics: In statistics, even numbers can be used in data analysis, particularly when calculating averages or medians, where the number of data points is even.

5. Everyday Life: Even numbers are commonly encountered in everyday life, such as in pairs (e.g., shoes, socks) and in situations where items are grouped in twos.

Conclusion

In conclusion, even numbers are a fundamental concept in mathematics characterized by their divisibility by 2. They possess unique properties and play a significant role in various mathematical operations and applications. Understanding even numbers, their classifications, and their interactions with other numbers is essential for solving mathematical problems and for applications in real-world scenarios. Through detailed explanations and illustrative examples, we can appreciate the significance of even numbers in both theoretical and practical contexts, showcasing their importance in the broader landscape of mathematics. Whether in arithmetic, algebra, or everyday life, even numbers remain a cornerstone of numerical understanding.

Blog.Pengayaan.Com