Force is a fundamental concept in physics that describes the interaction between objects that can cause a change in motion. It is a vector quantity, meaning it has both magnitude and direction. Understanding force is essential for analyzing the behavior of objects in motion, predicting their trajectories, and solving problems in mechanics. This article aims to provide an exhaustive overview of force, detailing its definition, types, laws, calculation methods, and applications, along with illustrative explanations of each concept.
Understanding Force
1. Definition of Force
In physics, force is defined as any interaction that, when unopposed, will change the motion of an object. It can cause an object to accelerate, decelerate, change direction, or deform. The standard unit of force in the International System of Units (SI) is the newton (N), where 
. This means that one newton is the force required to accelerate a one-kilogram mass by one meter per second squared.
- Illustrative Explanation: Imagine pushing a shopping cart. When you apply a force to the cart, it starts to move. If you push harder, it accelerates faster. Just as the strength of your push determines how quickly the cart moves, the concept of force quantifies the influence that causes changes in motion.
2. Types of Force
Forces can be categorized into several types based on their nature and the interactions they represent. The most common types include contact forces and non-contact forces.
a. Contact Forces
Contact forces are those that occur when two objects are physically touching each other. They include:
- Frictional Force: The force that opposes the relative motion of two surfaces in contact. It acts parallel to the surfaces and can be static (preventing motion) or kinetic (opposing motion).
– Illustrative Explanation: Consider trying to slide a heavy box across the floor. The frictional force between the box and the floor resists your push, making it harder to move. Just as friction slows down the box, it plays a crucial role in everyday motion.
- Normal Force: The force exerted by a surface that supports the weight of an object resting on it. It acts perpendicular to the surface.
– Illustrative Explanation: Imagine a book resting on a table. The table exerts an upward normal force equal to the weight of the book, preventing it from falling through. Just as the table supports the book, the normal force is essential for maintaining equilibrium.
- Tension Force: The force transmitted through a string, rope, or cable when it is pulled tight by forces acting at either end.
– Illustrative Explanation: Picture a tug-of-war game. The tension in the rope is the force that both teams exert on the rope, trying to pull it toward themselves. Just as the tension keeps the rope taut, it is a key factor in understanding forces in connected systems.
- Applied Force: The force that is applied to an object by a person or another object.
– Illustrative Explanation: When you push a door to open it, you apply a force to the door. Just as your effort determines how easily the door opens, applied force is a fundamental concept in mechanics.
b. Non-Contact Forces
Non-contact forces are those that act at a distance without physical contact between objects. They include:
- Gravitational Force: The attractive force between two masses. It is proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
– Illustrative Explanation: Think of the Earth pulling you toward its center. This gravitational force keeps you grounded and is responsible for the motion of planets and satellites. Just as gravity affects everything with mass, it is a fundamental force in the universe.
- Electromagnetic Force: The force between charged particles. It can be attractive or repulsive, depending on the charges involved.
– Illustrative Explanation: Imagine two magnets. When you bring them close together, they either attract or repel each other based on their polarities. Just as the electromagnetic force governs the behavior of charged particles, it plays a crucial role in chemistry and electricity.
- Nuclear Force: The force that holds protons and neutrons together in the nucleus of an atom. It is a strong force that acts over very short distances.
– Illustrative Explanation: Consider the nucleus of an atom as a tightly packed group of protons and neutrons. The nuclear force is what keeps these particles bound together, overcoming the repulsive electromagnetic force between positively charged protons. Just as this force is essential for the stability of matter, it is a key concept in nuclear physics.
3. Newton’s Laws of Motion
Understanding force is closely tied to Newton’s Laws of Motion, which describe the relationship between force and motion. These laws are foundational principles in classical mechanics.
a. First Law (Law of Inertia)
An object at rest will remain at rest, and an object in motion will continue in motion with the same speed and in the same direction unless acted upon by a net external force.
- Illustrative Explanation: Imagine a soccer ball lying on the ground. It will not move unless someone kicks it (an external force). Similarly, a ball rolling on a smooth surface will keep rolling until friction or another force stops it. Just as inertia explains why objects resist changes in motion, it highlights the importance of force in initiating movement.
b. Second Law (Law of Acceleration)
The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This relationship can be expressed mathematically as:
![\[ F = ma \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f79f3c2eb337b5f747f4fa75f1b64907_l3.png "Rendered by QuickLaTeX.com")
Where:
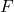is the net force,
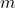is the mass of the object,
is the acceleration.- Illustrative Explanation: Consider pushing a car and a bicycle with the same force. The bicycle, being lighter, will accelerate more than the car. Just as the second law quantifies the relationship between force, mass, and acceleration, it helps us understand how different objects respond to applied forces.
c. Third Law (Action and Reaction)
For every action, there is an equal and opposite reaction. This means that when one object exerts a force on another, the second object exerts an equal force in the opposite direction on the first object.
- Illustrative Explanation: Imagine jumping off a small boat onto a dock. As you push down on the boat (action), the boat pushes you upward and backward (reaction). Just as this law explains the interactions between objects, it is fundamental to understanding motion in various contexts.
Calculation of Force
Calculating force involves using the appropriate formulas based on the context and the forces involved. Here are some examples:
1. Calculating Gravitational Force
The gravitational force between two masses can be calculated using Newton’s law of universal gravitation:
![\[ F_g = G \frac{m_1 m_2}{r^2} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-b3831eb58ed5da0a5db8d27b7d0d44ae_l3.png "Rendered by QuickLaTeX.com")
Where:
is the gravitational force,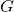
is the gravitational constant (
),
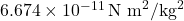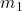and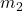 
are the masses,
is the distance between the centers of the two masses.
Example: If two objects with masses of 
and 
are separated by a distance of 
, the gravitational force can be calculated as follows:
![\[ F_g = 6.674 \times 10^{-11} \frac{(5)(10)}{(2)^2} = 8.3425 \times 10^{-10} \, \text{N} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-b26c1f98581078a1efd95cf0819d437e_l3.png "Rendered by QuickLaTeX.com")
- Illustrative Explanation: Just as the gravitational force between the two masses is determined by their masses and distance, this calculation illustrates how gravity operates at a distance.
2. Calculating Frictional Force
The frictional force can be calculated using the formula:
![\[ F_f = \mu F_n \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-33714cc2c01be3d3cf6b165006844be8_l3.png "Rendered by QuickLaTeX.com")
Where:
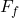is the frictional force,
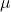is the coefficient of friction (a dimensionless value that represents the friction between two surfaces),
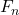is the normal force.
Example: If a box weighing 
is on a surface with a coefficient of friction of 
, the normal force is equal to the weight of the box (
). The frictional force can be calculated as follows:
![\[ F_f = 0.3 \times 196.2 = 58.86 \, \text{N} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-83b2d64281155477e6fce43d61373c9d_l3.png "Rendered by QuickLaTeX.com")
- Illustrative Explanation: Just as the frictional force opposes the motion of the box, this calculation shows how the coefficient of friction and the normal force determine the resistance to motion.
3. Calculating Net Force
The net force acting on an object can be calculated by summing all the individual forces acting on it, taking into account their directions. If multiple forces are acting on an object, the net force can be expressed as:
![\[ F_{net} = F_1 + F_2 + F_3 + \ldots \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-202688cdf14c8672ddeaf2464910f511_l3.png "Rendered by QuickLaTeX.com")
Example: If a box is pulled to the right with a force of 
and pushed to the left with a force of 
, the net force can be calculated as follows:
![\[ F_{net} = 10 \, \text{N} - 4 \, \text{N} = 6 \, \text{N} \, \text{(to the right)} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-e2ea25ffe9b4c851454d587722ab44b6_l3.png "Rendered by QuickLaTeX.com")
- Illustrative Explanation: Just as the net force determines the overall motion of the box, this calculation illustrates how multiple forces interact to produce a resultant force.
Applications of Force
Force has numerous important applications across various fields, including engineering, physics, sports, and everyday life.
1. Engineering and Design
In engineering, understanding force is crucial for designing structures, machines, and systems. Engineers must consider the forces acting on components to ensure safety and functionality.
- Illustrative Explanation: Imagine designing a bridge. Engineers must calculate the forces acting on the bridge, including the weight of vehicles and environmental factors like wind. Just as understanding these forces ensures the bridge’s stability, force analysis is essential for safe engineering practices.
2. Physics and Motion Analysis
In physics, force is fundamental for analyzing motion and understanding the behavior of objects. It is used to derive equations of motion and predict the outcomes of various scenarios.
- Illustrative Explanation: Consider a projectile launched into the air. Physicists analyze the forces acting on the projectile, such as gravity and air resistance, to predict its trajectory. Just as this analysis helps understand motion, force is a key concept in physics.
3. Sports and Physical Activities
In sports, understanding force is essential for optimizing performance and preventing injuries. Athletes and coaches analyze the forces involved in movements to improve techniques and training.
- Illustrative Explanation: Think of a sprinter starting a race. The force exerted by their legs against the ground determines their acceleration. Just as optimizing this force leads to better performance, understanding force is vital for athletes.
4. Everyday Life
In everyday life, force is relevant in various situations, such as lifting objects, driving vehicles, and playing sports. Understanding force can help individuals make informed decisions about their activities.
- Illustrative Explanation: Imagine carrying groceries up a flight of stairs. The force you exert to lift the bags affects how quickly you can ascend. Just as understanding the forces involved helps you manage your load, force is a fundamental concept in daily activities.
Conclusion
In conclusion, force is a fundamental concept that plays a crucial role in understanding the interactions between objects and the changes in motion that result from these interactions. By exploring its definition, types, laws, calculation methods, and applications, we can appreciate the significance of force in various fields, from engineering and physics to sports and everyday life. As our understanding of force continues to evolve, we can harness this knowledge to improve designs, enhance performance, and optimize our interactions with the physical world. The study of force not only deepens our understanding of motion and energy but also highlights the intricate relationships between objects in our universe. Understanding force is essential for addressing challenges in science and engineering, paving the way for innovations that can benefit society as a whole.