Young’s Modulus – Blog.Pengayaan.Com

Young’s Modulus, also known as the tensile modulus or elastic modulus, is a fundamental property of materials that quantifies their ability to deform elastically (i.e., non-permanently) when subjected to stress. It is a critical parameter in the fields of materials science, engineering, and physics, as it provides insight into the stiffness and elasticity of materials. Understanding Young’s Modulus is essential for designing structures and components that can withstand various forces without undergoing permanent deformation. In this comprehensive exploration of Young’s Modulus, we will delve into its definition, mathematical formulation, significance, applications, and the factors that influence it.

Definition of Young’s Modulus

Young’s Modulus ( $E$ ) is defined as the ratio of tensile stress to tensile strain in a material within the elastic limit. It describes how much a material will deform under a given load and is a measure of the stiffness of the material. Mathematically, Young’s Modulus can be expressed as:

$E = \frac{\sigma}{\epsilon}$

Where:

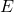$E$ is Young’s Modulus (in pascals, Pa).
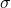$\sigma$ is the tensile stress (in pascals, Pa), defined as the force ( 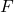$F$ ) applied per unit area ( $A$ ):

$\sigma = \frac{F}{A}$

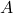$\epsilon$ is the tensile strain (dimensionless), defined as the change in length (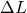 $\Delta L$ ) divided by the original length ( $L_0$ ):

$\epsilon = \frac{\Delta L}{L_0}$

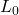Significance of Young’s Modulus

Young’s Modulus is a crucial parameter in engineering and materials science for several reasons:

1. Material Selection: Young’s Modulus helps engineers and designers select appropriate materials for specific applications based on their stiffness and ability to withstand loads without deforming.

2. Structural Analysis: In structural engineering, Young’s Modulus is used to analyze how structures will respond to applied loads. It allows for the calculation of deflections and stresses in beams, columns, and other structural elements.

3. Predicting Behavior: Understanding Young’s Modulus enables predictions about how materials will behave under different loading conditions, which is essential for ensuring safety and performance in engineering applications.

4. Quality Control: Young’s Modulus can be used as a quality control measure in manufacturing processes. Consistency in Young’s Modulus values can indicate uniformity in material properties.

Applications of Young’s Modulus

Young’s Modulus has a wide range of applications across various fields, including:

1. Civil Engineering: In civil engineering, Young’s Modulus is used to design and analyze structures such as bridges, buildings, and dams. It helps determine how much a structure will deflect under load and ensures that it can safely support the intended loads.

2. Mechanical Engineering: In mechanical engineering, Young’s Modulus is essential for designing components such as shafts, beams, and springs. It is used to calculate stresses and strains in mechanical systems.

3. Aerospace Engineering: In aerospace applications, materials must withstand significant forces while maintaining structural integrity. Young’s Modulus is critical for selecting materials that can endure the stresses experienced during flight.

4. Manufacturing: In manufacturing processes, Young’s Modulus is used to evaluate the performance of materials under various conditions, such as machining, forming, and welding.

5. Biomedical Engineering: In biomedical applications, Young’s Modulus is important for designing implants and prosthetics that must mimic the mechanical properties of natural tissues.

Factors Influencing Young’s Modulus

Several factors can influence the value of Young’s Modulus for a given material:

1. Material Composition: The chemical composition and microstructure of a material significantly affect its Young’s Modulus. For example, metals typically have higher Young’s Modulus values than polymers due to their atomic structure and bonding.

2. Temperature: Young’s Modulus can vary with temperature. Generally, as temperature increases, the stiffness of materials decreases, leading to lower Young’s Modulus values.

3. Strain Rate: The rate at which a material is deformed can also affect its Young’s Modulus. Some materials exhibit strain rate sensitivity, meaning their stiffness changes with the speed of loading.

4. Anisotropy: Many materials, especially composites and crystals, exhibit anisotropic behavior, meaning their mechanical properties vary with direction. Young’s Modulus can differ based on the orientation of the material.

5. Defects and Impurities: The presence of defects, impurities, or inclusions in a material can alter its mechanical properties, including Young’s Modulus. High-quality materials with fewer defects typically exhibit more consistent Young’s Modulus values.

Measurement of Young’s Modulus

Young’s Modulus can be measured using various experimental techniques, including:

1. Tensile Testing: In tensile testing, a sample is subjected to a uniaxial tensile load, and the resulting stress and strain are measured. The slope of the linear portion of the stress-strain curve provides the value of Young’s Modulus.

2. Flexural Testing: In flexural testing, a beam is subjected to a bending load, and the resulting deflection is measured. Young’s Modulus can be calculated based on the geometry of the beam and the applied load.

3. Dynamic Mechanical Analysis (DMA): This technique involves applying an oscillatory load to a material and measuring its response. Young’s Modulus can be determined from the material’s storage and loss moduli.

4. Ultrasonic Testing: Ultrasonic waves can be used to measure the velocity of sound in a material, which can be related to Young’s Modulus through the material’s density.

Conclusion

In conclusion, Young’s Modulus is a fundamental property of materials that quantifies their ability to deform elastically under stress. Its definition, mathematical formulation, significance, applications, and influencing factors provide a comprehensive understanding of how materials behave under various loading conditions. From civil and mechanical engineering to aerospace and biomedical applications, Young’s Modulus plays a critical role in the design and analysis of structures and components. As research and technology continue to evolve, the study of Young’s Modulus will remain a vital area of exploration, driving advancements in materials science and engineering. Understanding Young’s Modulus not only enhances our knowledge of material behavior but also informs practical applications that impact our daily lives and the development of new technologies.

Blog.Pengayaan.Com