Gauss’s Law – Blog.Pengayaan.Com

Gauss’s Law is a fundamental principle in electromagnetism that relates the electric field in a region to the charge distribution that produces it. Named after the German mathematician and physicist Carl Friedrich Gauss, this law is a cornerstone of electrostatics and is integral to understanding electric fields and their behavior in various physical situations. Gauss’s Law is not only essential for theoretical physics but also has practical applications in engineering, electronics, and various technologies. This article aims to provide an exhaustive overview of Gauss’s Law, including its mathematical formulation, physical significance, applications, and implications in both electrostatics and magnetism.

Definition of Gauss’s Law

Gauss’s Law states that the electric flux ( $\Phi_E$ ) through a closed surface is directly proportional to the total electric charge ( $Q_{\text{enc}}$ ) enclosed within that surface. Mathematically, Gauss’s Law can be expressed as:

$\Phi_E = \oint_S \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{\text{enc}}}{\varepsilon_0}$

Where:

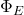$\Phi_E$ is the electric flux through the closed surface 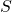$S$ (measured in newton-meters squared per coulomb, N·m²/C),
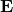$\mathbf{E}$ is the electric field vector (measured in volts per meter, V/m),
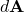$d\mathbf{A}$ is the differential area vector on the closed surface 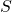$S$ (measured in square meters, m²),
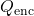$Q_{\text{enc}}$ is the total charge enclosed within the surface (measured in coulombs, C),
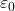$\varepsilon_0$ is the permittivity of free space, approximately equal to $8.854 \times 10^{-12} \, \text{C}^2/\text{N·m}^2$ .

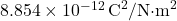Understanding Electric Flux

To fully grasp Gauss’s Law, it is essential to understand the concept of electric flux:

1. Electric Field ( $\mathbf{E}$ ): The electric field is a vector field that represents the force experienced by a unit positive charge placed in the field. It is defined as the force per unit charge and is directed away from positive charges and toward negative charges.

2. Electric Flux ( $\Phi_E$ ): Electric flux quantifies the number of electric field lines passing through a given surface. It is calculated as the dot product of the electric field vector and the area vector, integrated over the entire closed surface. The area vector $d\mathbf{A}$ is perpendicular to the surface and has a magnitude equal to the area of the differential element.

3. Closed Surface: A closed surface is a three-dimensional boundary that completely encloses a volume. Examples include spheres, cubes, and cylinders. The choice of closed surface is crucial in applying Gauss’s Law.

Physical Significance of Gauss’s Law

Gauss’s Law has profound implications in electrostatics and provides insights into the behavior of electric fields:

1. Charge Distribution: Gauss’s Law allows us to determine the electric field produced by symmetric charge distributions, such as point charges, infinite planes, and spherical shells. By choosing an appropriate Gaussian surface, we can simplify calculations and derive the electric field without directly integrating the contributions from individual charges.

2. Field Lines: The law illustrates the relationship between electric field lines and charge distribution. A higher density of electric field lines indicates a stronger electric field, while the total number of lines passing through a closed surface is proportional to the enclosed charge.

3. Conservation of Charge: Gauss’s Law is consistent with the principle of charge conservation. If the total charge within a closed surface changes, the electric flux through that surface will also change accordingly.

Applications of Gauss’s Law

Gauss’s Law is widely used in various applications across physics and engineering:

1. Calculating Electric Fields: Gauss’s Law simplifies the calculation of electric fields for symmetric charge distributions. Common scenarios include:

Point Charge: For a point charge 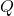$Q$ located at the center of a spherical Gaussian surface of radius $r$ :

$E = \frac{Q}{4\pi \varepsilon_0 r^2}$

Infinite Plane Charge: For an infinite plane with surface charge density $\sigma$ :

$E = \frac{\sigma}{2\varepsilon_0}$

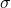Spherical Shell: For a uniformly charged spherical shell, the electric field outside the shell behaves as if all the charge were concentrated at the center, while inside the shell, the electric field is zero.

2. Capacitance: Gauss’s Law is used to derive the capacitance of parallel plate capacitors. The electric field between the plates can be calculated using Gauss’s Law, leading to the expression for capacitance:

$C = \frac{\varepsilon_0 A}{d}$

Where $A$ is the area of the plates and $d$ is the separation between them.

3. Electrostatics in Conductors: Gauss’s Law helps explain the behavior of electric fields in conductors. In electrostatic equilibrium, the electric field inside a conductor is zero, and any excess charge resides on the surface. This principle is crucial for understanding shielding and the behavior of charged conductors.

4. Magnetism: While Gauss’s Law is primarily associated with electric fields, a similar law exists for magnetic fields, known as Gauss’s Law for Magnetism. It states that the total magnetic flux through a closed surface is zero, indicating that magnetic field lines are continuous and do not begin or end at any point.

Implications of Gauss’s Law

Gauss’s Law has several important implications in both theoretical and practical contexts:

1. Symmetry: The power of Gauss’s Law lies in its ability to exploit symmetry. When dealing with symmetric charge distributions, such as spherical, cylindrical, or planar symmetries, Gauss’s Law allows for straightforward calculations of electric fields without complex integrals.

2. Field Behavior: Gauss’s Law provides insights into how electric fields behave in the presence of charges. For example, it shows that the electric field decreases with distance from a point charge and remains constant near an infinite plane of charge.

3. Electromagnetic Theory: Gauss’s Law is one of Maxwell’s equations, which form the foundation of classical electromagnetism. It is essential for understanding the interplay between electric and magnetic fields and their role in electromagnetic waves.

4. Engineering Applications: Engineers use Gauss’s Law in the design of electrical devices, such as capacitors, sensors, and shielding materials. Understanding electric fields and their behavior is crucial for ensuring the safety and efficiency of electrical systems.

Conclusion

Gauss’s Law is a fundamental principle in electromagnetism that provides a powerful tool for understanding electric fields and their relationship to charge distributions. Its mathematical formulation and physical significance make it essential for both theoretical and practical applications in physics and engineering. By leveraging the symmetry of charge distributions, Gauss’s Law simplifies the calculation of electric fields and enhances our understanding of electrostatics. As one of Maxwell’s equations, Gauss’s Law is integral to the broader framework of electromagnetism, influencing various technologies and scientific advancements. The ongoing study of Gauss’s Law and its applications continues to shape our understanding of electric phenomena and contributes to the development of innovative solutions in electrical engineering, telecommunications, and beyond.

Blog.Pengayaan.Com