Helmholtz Free Energy – Blog.Pengayaan.Com

Helmholtz free energy, denoted as $A$ or $F$ , is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at constant temperature and volume. Named after the German physicist Hermann von Helmholtz, this concept is crucial in understanding the behavior of systems in thermodynamics, particularly in the context of chemical reactions, phase transitions, and statistical mechanics. This article will delve into the definition, mathematical formulation, significance, applications, and limitations of Helmholtz free energy, providing a thorough understanding of this essential concept, complete with illustrative explanations to enhance comprehension.

Definition of Helmholtz Free Energy

Helmholtz free energy is defined as the difference between the internal energy of a system and the product of its temperature and entropy. Mathematically, it can be expressed as:

$A = U - TS$

Where:

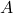$A$ is the Helmholtz free energy.
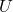$U$ is the internal energy of the system.
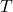$T$ is the absolute temperature (in Kelvin).
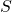$S$ is the entropy of the system.

Illustrative Explanation: Imagine a battery that stores energy. The internal energy $U$ represents the total energy stored in the battery, while the product $TS$ represents the energy that is “lost” to disorder (entropy) at a given temperature. The Helmholtz free energy $A$ represents the energy available to do useful work, akin to the energy you can actually use from the battery after accounting for the energy lost to disorder.

Mathematical Formulation

The Helmholtz free energy can be derived from the first and second laws of thermodynamics. The first law states that energy cannot be created or destroyed, while the second law introduces the concept of entropy, which quantifies the amount of energy in a system that is unavailable to do work.

Differential Form

The differential form of Helmholtz free energy can be expressed as:

$dA = -SdT - PdV$

Where:

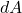$dA$ is the change in Helmholtz free energy.
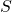$S$ is the entropy.
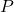$P$ is the pressure.
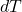$dT$ is the change in temperature.
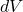$dV$ is the change in volume.

Illustrative Explanation: Consider a balloon filled with air. If you change the temperature (by heating or cooling) or change the volume (by squeezing or expanding), the Helmholtz free energy will change accordingly. The equation shows how these changes affect the energy available for work in the system.

Relation to Other Thermodynamic Potentials

Helmholtz free energy is one of several thermodynamic potentials, including Gibbs free energy, internal energy, and enthalpy. Each of these potentials is useful in different contexts. For example, Gibbs free energy is more relevant for processes occurring at constant temperature and pressure, while Helmholtz free energy is more applicable to systems at constant temperature and volume.

Illustrative Explanation: Think of different tools in a toolbox. Just as you would choose a hammer for driving nails and a screwdriver for turning screws, you would choose Helmholtz free energy for systems at constant temperature and volume, while Gibbs free energy is better suited for constant temperature and pressure scenarios.

Significance of Helmholtz Free Energy

Helmholtz free energy is significant for several reasons:

1. Indicator of Spontaneity

The change in Helmholtz free energy ( $\Delta A$ ) during a process indicates whether the process can occur spontaneously at constant temperature and volume. If $\Delta A < 0$ , the process is spontaneous; if $\Delta A > 0$ , the process is non-spontaneous.

Illustrative Explanation: Imagine a ball rolling down a hill. If the ball rolls downhill (spontaneous process), it represents a decrease in Helmholtz free energy. Conversely, if you want to roll the ball uphill (non-spontaneous process), you need to exert energy, indicating an increase in Helmholtz free energy.

2. Useful Work Calculation

Helmholtz free energy provides a measure of the maximum useful work obtainable from a system at constant temperature and volume. This is particularly important in chemical reactions and physical processes.

Illustrative Explanation: Consider a wind-up toy. The energy stored in the spring (analogous to internal energy) can be released to do work (move the toy). However, some energy is lost to friction and disorder (entropy). The Helmholtz free energy represents the energy available to make the toy move, illustrating how it quantifies useful work.

3. Connection to Statistical Mechanics

In statistical mechanics, Helmholtz free energy is related to the partition function, which describes the statistical properties of a system in thermodynamic equilibrium. This connection allows for the calculation of thermodynamic properties from microscopic states.

Illustrative Explanation: Imagine a box filled with gas molecules. The Helmholtz free energy can be thought of as a way to summarize the behavior of all those molecules and their interactions, similar to how a summary of a book captures the main themes and ideas without detailing every single page.

Applications of Helmholtz Free Energy

Helmholtz free energy has numerous practical applications across various fields, including:

1. Chemical Reactions

In chemistry, Helmholtz free energy is used to predict the spontaneity of chemical reactions at constant temperature and volume. It helps chemists understand which reactions are favorable and how to optimize reaction conditions.

Illustrative Explanation: Imagine a chemist mixing reactants in a flask. By calculating the change in Helmholtz free energy, the chemist can determine whether the reaction will proceed spontaneously, similar to deciding whether to jump into a pool based on the water temperature.

2. Phase Transitions

Helmholtz free energy is crucial in studying phase transitions, such as melting, boiling, and sublimation. It helps predict the conditions under which a substance will change from one phase to another.

Illustrative Explanation: Consider ice melting into water. The Helmholtz free energy can be used to determine the temperature and pressure conditions under which this phase transition occurs, much like understanding the right conditions for a plant to bloom.

3. Material Science

In material science, Helmholtz free energy is used to analyze the stability of materials and predict their behavior under different conditions. This is essential for developing new materials with desired properties.

Illustrative Explanation: Think of a materials engineer designing a new alloy. By calculating the Helmholtz free energy of different compositions, the engineer can determine which combination will yield the strongest and most stable material, similar to a chef experimenting with ingredients to create the perfect dish.

4. Biological Systems

In biology, Helmholtz free energy is used to study metabolic processes and the energetics of biochemical reactions. It helps researchers understand how living organisms convert energy and maintain homeostasis.

Illustrative Explanation: Imagine a cell converting glucose into energy. The Helmholtz free energy can be used to analyze the efficiency of this process, much like evaluating how effectively a car converts fuel into motion.

Limitations of Helmholtz Free Energy

While Helmholtz free energy is a valuable concept, there are limitations to consider:

1. Constant Temperature and Volume Assumption

Helmholtz free energy is only applicable under conditions of constant temperature and volume. In many real-world processes, these conditions may not be met, limiting the applicability of this potential.

Illustrative Explanation: Think of a balloon being inflated. As you blow air into it, both the temperature and volume change. In this case, using Helmholtz free energy to analyze the process would be inappropriate, similar to trying to use a recipe designed for baking a cake to make a smoothie.

2. Complexity of Real Systems

Real systems often exhibit complex behaviors that may not be accurately described by Helmholtz free energy alone. Interactions between components, non-ideal behavior, and external influences can complicate analyses.

Illustrative Explanation: Imagine trying to predict the weather. While you can use models to estimate temperature and pressure, the actual weather is influenced by numerous factors, making it difficult to predict accurately. Similarly, real systems may not conform neatly to the predictions made using Helmholtz free energy.

3. Limited to Closed Systems

Helmholtz free energy is applicable primarily to closed systems, where no mass is exchanged with the surroundings. In open systems, where mass and energy can flow in and out, other thermodynamic potentials may be more appropriate.

Illustrative Explanation: Consider a swimming pool. If you add water (mass) to the pool, the conditions change, and the analysis becomes more complex. In this case, using Helmholtz free energy to describe the system would be inadequate, similar to trying to analyze a dynamic situation with a static model.

Conclusion

In conclusion, Helmholtz free energy is a fundamental concept in thermodynamics that measures the useful work obtainable from a closed system at constant temperature and volume. By understanding the definition, mathematical formulation, significance, applications, and limitations of Helmholtz free energy, we gain valuable insights into this essential concept. Helmholtz free energy plays a critical role in various scientific fields, including chemistry, material science, and biology, helping researchers and practitioners analyze processes, predict behaviors, and optimize conditions. As we continue to explore the intricacies of thermodynamic principles, Helmholtz free energy will remain a vital tool for understanding the energy transformations that govern the natural world. Through ongoing research and development, the principles governing Helmholtz free energy will continue to evolve, contributing to advancements in science and technology while enhancing our understanding of complex systems.

Blog.Pengayaan.Com