Understanding Horizontal Lines: A Comprehensive Guide

Horizontal lines are fundamental concepts in geometry and mathematics, serving as a basis for understanding various geometric shapes, graphs, and real-world applications. This article will provide a detailed exploration of horizontal lines, including their definition, properties, equations, graphical representation, and applications, along with illustrative examples to enhance understanding.

Definition of a Horizontal Line

A horizontal line is a straight line that runs parallel to the x-axis in a Cartesian coordinate system. It has a constant y-coordinate, meaning that for any point on the line, the y-value remains the same while the x-value can vary. In mathematical terms, a horizontal line can be expressed as:

$y = b$

Where:

$y$ is the constant y-coordinate of the line.
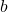$b$ is a real number representing the y-value at which the line is located.

Illustrative Example: If we have a horizontal line at $y = 3$ , this means that no matter what value $x$ takes, the y-coordinate will always be 3. Thus, points on this line include $(0, 3)$ , $(1, 3)$ , $(-2, 3)$ , and so on.

Properties of Horizontal Lines

Horizontal lines possess several key properties that distinguish them from other types of lines:

1. Slope: The slope of a horizontal line is always zero. This is because the change in y (rise) is zero while the change in x (run) can be any non-zero value. Mathematically, the slope $m$ is defined as:

$m = \frac{\Delta y}{\Delta x} = \frac{0}{\Delta x} = 0$

2. Equation: The equation of a horizontal line is always in the form $y = b$ , where $b$ is a constant. This indicates that the line does not rise or fall as it moves along the x-axis.

3. Graphical Representation: When graphed on a Cartesian plane, a horizontal line appears as a straight line that extends infinitely in both directions along the x-axis, remaining at the same height (y-value).

4. Intersection with Axes: A horizontal line intersects the y-axis at the point $(0, b)$ and does not intersect the x-axis unless $b = 0$ , in which case it coincides with the x-axis.

5. Parallel Lines: Any two horizontal lines are parallel to each other, as they have the same slope (zero) and never intersect.

Graphical Representation of Horizontal Lines

To visualize a horizontal line, consider the following diagram:

“`
y
|
|      +——————- (y = b)
|      |
|      |
|      |
+—————————— x
“`

In this diagram, the horizontal line is represented at a constant height $b$ on the y-axis. The line extends infinitely to the left and right along the x-axis.

Examples of Horizontal Lines

1. Example 1: A horizontal line at $y = 2$ :
– The equation is $y = 2$ .
– Points on this line include $(0, 2)$ , $(1, 2)$ , $(-3, 2)$ , etc.

2. Example 2: A horizontal line at $y = -1$ :
– The equation is $y = -1$ .
– Points on this line include $(0, -1)$ , $(2, -1)$ , $(-5, -1)$ , etc.

3. Example 3: The x-axis itself is a horizontal line represented by the equation $y = 0$ :
– This line intersects the y-axis at the origin $(0, 0)$ and extends infinitely in both directions along the x-axis.

Applications of Horizontal Lines

Horizontal lines have numerous applications across various fields:

1. Mathematics: In algebra and geometry, horizontal lines are used to represent constant values and to analyze relationships between variables. They are essential in graphing functions and understanding linear equations.

2. Graphing Functions: When graphing functions, horizontal lines can represent constant functions, where the output value does not change regardless of the input. For example, the function $f(x) = 5$ is represented by a horizontal line at $y = 5$ .

3. Architecture and Engineering: In architecture and engineering, horizontal lines are used in design and construction to ensure that structures are level and balanced. They are crucial in creating blueprints and plans for buildings.

4. Art and Design: Artists often use horizontal lines to create a sense of stability and calmness in their compositions. In design, horizontal lines can guide the viewer’s eye and create visual balance.

5. Navigation and Mapping: In navigation, horizontal lines can represent latitude lines on maps, indicating constant distances north or south of the equator.

Conclusion

In conclusion, horizontal lines are a fundamental concept in geometry characterized by their constant y-coordinate and zero slope. They play a significant role in mathematics, graphing, architecture, art, and various real-world applications. Understanding the properties, equations, and graphical representations of horizontal lines is essential for solving mathematical problems and for applications in diverse fields. Through detailed explanations and illustrative examples, we can appreciate the significance of horizontal lines in both theoretical and practical contexts, showcasing their importance in the broader landscape of mathematics and design. Whether in graphing functions, constructing buildings, or creating art, horizontal lines remain a cornerstone of geometric understanding.

Blog.Pengayaan.Com