The Ideal Gas Equation: A Comprehensive Exploration

The Ideal Gas Equation is a fundamental relationship in chemistry and physics that describes the behavior of ideal gases. It combines several key properties of gases—pressure, volume, temperature, and the number of moles—into a single equation. This equation is essential for understanding gas behavior under various conditions and serves as a foundation for more complex gas laws and real gas behavior. This article will delve into the definition, derivation, components, applications, and limitations of the Ideal Gas Equation, providing a thorough understanding of this crucial concept in science, complete with illustrative explanations to enhance comprehension.

Definition of the Ideal Gas Equation

The Ideal Gas Equation is expressed mathematically as:

$PV = nRT$

Where:

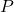$P$ = Pressure of the gas (in atmospheres, pascals, or other units)
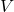$V$ = Volume of the gas (in liters or cubic meters)
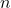$n$ = Number of moles of the gas
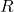$R$ = Ideal gas constant (0.0821 L·atm/(K·mol) or 8.314 J/(K·mol))
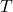$T$ = Temperature of the gas (in Kelvin)

This equation relates the four primary properties of an ideal gas, allowing for calculations and predictions about gas behavior.

Illustrative Explanation: Imagine a balloon filled with air. The pressure inside the balloon (P) pushes against the walls, the volume (V) is the space the air occupies, the number of air molecules (n) corresponds to the amount of air, and the temperature (T) reflects how energetic those air molecules are. The Ideal Gas Equation helps us understand how these factors interact to determine the behavior of the gas in the balloon.

Derivation of the Ideal Gas Equation

The Ideal Gas Equation can be derived from several empirical gas laws, including Boyle’s Law, Charles’s Law, and Avogadro’s Law. Here’s a brief overview of each law and how they contribute to the Ideal Gas Equation:

1. Boyle’s Law

Boyle’s Law states that the pressure of a gas is inversely proportional to its volume when the temperature and the number of moles are held constant:

$P \propto \frac{1}{V} \quad \text{or} \quad PV = k_1$

Where $k_1$ is a constant.

2. Charles’s Law

Charles’s Law states that the volume of a gas is directly proportional to its absolute temperature when the pressure and the number of moles are held constant:

$V \propto T \quad \text{or} \quad \frac{V}{T} = k_2$

Where $k_2$ is a constant.

3. Avogadro’s Law

Avogadro’s Law states that the volume of a gas is directly proportional to the number of moles when the pressure and temperature are held constant:

$V \propto n \quad \text{or} \quad \frac{V}{n} = k_3$

Where $k_3$ is a constant.

Combining the Laws

By combining these three laws, we can derive the Ideal Gas Equation. From Boyle’s Law, we can express pressure in terms of volume and a constant. From Charles’s Law, we can express volume in terms of temperature. Finally, from Avogadro’s Law, we can express volume in terms of the number of moles. When these relationships are combined, we arrive at the Ideal Gas Equation:

$PV = nRT$

Illustrative Explanation: Think of these laws as building blocks. Boyle’s Law provides the foundation (pressure and volume), Charles’s Law adds height (volume and temperature), and Avogadro’s Law fills in the space (volume and moles). When combined, they create a complete structure (the Ideal Gas Equation) that describes gas behavior.

Components of the Ideal Gas Equation

1. Pressure (P)

Pressure is defined as the force exerted by gas molecules colliding with the walls of their container. It is typically measured in units such as atmospheres (atm), pascals (Pa), or millimeters of mercury (mmHg).

Illustrative Explanation: Imagine a group of children playing basketball in a small room. As they bounce the ball, it hits the walls, creating pressure. The more children there are (more gas molecules), the more pressure is exerted on the walls.

2. Volume (V)

Volume is the amount of space that a gas occupies, usually measured in liters (L) or cubic meters (m³). The volume of a gas can change significantly with changes in pressure and temperature.

Illustrative Explanation: Picture a balloon. When you blow air into it, the volume of the balloon increases. If you squeeze the balloon, the volume decreases. This illustrates how gas volume can change based on external conditions.

3. Number of Moles (n)

The number of moles represents the quantity of gas present in a sample. One mole of any substance contains approximately $6.022 \times 10^{23}$ particles (Avogadro’s number).

Illustrative Explanation: Imagine a jar filled with marbles. Each marble represents a molecule of gas. The total number of marbles in the jar corresponds to the number of moles of gas. More marbles mean more gas molecules.

4. Ideal Gas Constant (R)

The ideal gas constant (R) is a proportionality constant that relates the other variables in the Ideal Gas Equation. Its value depends on the units used for pressure, volume, and temperature. Common values include:

$R = 0.0821 \, \text{L·atm/(K·mol)}$
$R = 8.314 \, \text{J/(K·mol)}$

Illustrative Explanation: Think of R as a conversion factor that helps you translate between different units of measurement. Just as a recipe might call for specific measurements (cups, tablespoons), R helps ensure that the equation works correctly with the units you choose.

5. Temperature (T)

Temperature is a measure of the average kinetic energy of gas molecules and is always expressed in Kelvin (K) in the Ideal Gas Equation. To convert from Celsius to Kelvin, add 273.15.

Illustrative Explanation: Imagine a group of children running around. The faster they run (higher temperature), the more energetic they are. In gas terms, higher temperatures mean faster-moving molecules, which increases pressure if the volume is constant.

Applications of the Ideal Gas Equation

The Ideal Gas Equation has numerous applications in both theoretical and practical contexts:

1. Calculating Gas Properties

The Ideal Gas Equation allows chemists and physicists to calculate unknown properties of gases, such as pressure, volume, temperature, or the number of moles, given the other three variables.

Illustrative Explanation: Think of a detective solving a mystery. By knowing three clues (pressure, volume, temperature), the detective can deduce the fourth clue (number of moles) to complete the picture.

2. Stoichiometry of Gas Reactions

The Ideal Gas Equation is used in stoichiometric calculations involving gases, allowing chemists to predict the amounts of reactants and products in gas-phase reactions.

Illustrative Explanation: Imagine a chef preparing a meal. By knowing the recipe (stoichiometry) and the amount of one ingredient (gas), the chef can determine how much of the other ingredients (gases) are needed to complete the dish.

3. Real-World Applications

The Ideal Gas Equation is applied in various fields, including engineering, meteorology, and environmental science. For example, it helps engineers design gas storage tanks and predict the behavior of gases in different conditions.

Illustrative Explanation: Picture an engineer designing a gas tank. By using the Ideal Gas Equation, they can ensure that the tank can safely hold the gas at different temperatures and pressures, much like a builder ensuring a structure can withstand various weather conditions.

Limitations of the Ideal Gas Equation

While the Ideal Gas Equation is a powerful tool, it has limitations:

1. Ideal vs. Real Gases

The Ideal Gas Equation assumes that gases behave ideally, meaning that gas molecules do not interact with each other and occupy no volume. However, real gases deviate from this behavior under high pressure and low temperature, where intermolecular forces and molecular volume become significant.

Illustrative Explanation: Imagine a group of friends in a small car (real gas). When the car is full (high pressure), they start to feel cramped (deviations from ideal behavior). In contrast, when they are in a spacious van (ideal gas), they can move freely without feeling crowded.

2. High Pressure and Low Temperature

At high pressures, gas molecules are forced closer together, leading to increased intermolecular forces. At low temperatures, gas molecules have less kinetic energy, which can also lead to deviations from ideal behavior.

Illustrative Explanation: Think of a crowded concert where people are packed tightly together (high pressure). They can’t move freely, and their interactions become more significant. Conversely, at a picnic in a large park (low temperature), people have more space and can move around easily, resembling ideal gas behavior.

3. Non-ideal Gas Behavior

Certain gases, such as water vapor and carbon dioxide, exhibit non-ideal behavior due to strong intermolecular forces. In such cases, more complex equations, such as the Van der Waals equation, are used to describe gas behavior more accurately.

Illustrative Explanation: Imagine a group of friends who are very close (strong intermolecular forces). They interact more than a group of acquaintances (ideal gas), leading to different dynamics. In this case, a more nuanced approach is needed to understand their interactions.

Conclusion

In conclusion, the Ideal Gas Equation is a fundamental relationship that describes the behavior of ideal gases by relating pressure, volume, temperature, and the number of moles. By understanding the components, derivation, applications, and limitations of the Ideal Gas Equation, we gain valuable insights into gas behavior and its implications in various scientific fields. The Ideal Gas Equation serves as a cornerstone for further studies in thermodynamics, physical chemistry, and engineering. As we continue to explore the intricacies of gas behavior, we unlock new possibilities for innovation and discovery, ultimately enriching our understanding of the natural world and its complex chemical processes. Through ongoing research and development, the principles of the Ideal Gas Equation will continue to play a vital role in shaping the future of science and technology, contributing to solutions that address global challenges and improve our quality of life.

Blog.Pengayaan.Com