In electrical engineering, understanding the behavior of alternating current (AC) circuits is crucial for designing and analyzing various electronic systems. One of the fundamental concepts in AC circuit analysis is impedance, particularly in series LCR (Inductor-Capacitor-Resistor) circuits. This article will explore the definition of impedance, the characteristics of series LCR circuits, the calculation of impedance, and its significance in AC circuits, providing illustrative explanations to clarify each concept.
What is Impedance?
Definition
Impedance (Z) is a complex quantity that represents the total opposition that a circuit offers to the flow of alternating current. It combines both resistance (R) and reactance (X) into a single measure. Impedance is expressed in ohms (Ω) and is represented as:
![\[ Z = R + jX \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-05c15926e366fefd3f7f4cae010455e1_l3.png "Rendered by QuickLaTeX.com")
Where:
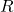is the resistance,
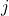is the imaginary unit (representing a 90-degree phase shift),
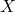is the reactance, which can be further divided into inductive reactance (
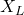) and capacitive reactance (
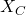).- Illustrative Explanation: Think of impedance as a combination of a road’s surface (resistance) and its curves and hills (reactance). Just as a smooth road allows for easy travel, resistance allows current to flow, while the curves and hills (reactance) affect how quickly and efficiently the current can move.
Historical Context
The concept of impedance emerged from the study of AC circuits in the late 19th century, as scientists and engineers sought to understand the behavior of electrical systems under alternating current. The term “impedance” was coined by Oliver Heaviside, who contributed significantly to the field of electrical engineering. The development of impedance analysis has since become a cornerstone of circuit theory and design.
- Illustrative Explanation: Imagine the evolution of a language. Just as words and phrases develop over time to convey complex ideas, the concept of impedance has evolved to help engineers describe the intricate behavior of AC circuits.
Characteristics of Series LCR Circuits
A series LCR circuit consists of three primary components connected in series: a resistor (R), an inductor (L), and a capacitor (C). Each component contributes to the overall impedance of the circuit.
1. Resistor (R)
The resistor provides resistance to the flow of current, dissipating energy in the form of heat. The resistance is constant and does not change with frequency.
- Illustrative Explanation: Think of a resistor as a narrow section of a water pipe. Just as the narrow section restricts the flow of water, the resistor limits the flow of electric current.
2. Inductor (L)
The inductor stores energy in a magnetic field when current flows through it. The inductive reactance () is frequency-dependent and is given by the formula:
![\[ X_L = 2\pi f L \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-43aed5fdb59be70875d6303ca7b01794_l3.png "Rendered by QuickLaTeX.com")
Where:
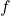is the frequency of the AC signal,
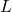is the inductance in henries (H).- Illustrative Explanation: Imagine a spring that compresses when you push it. The inductor resists changes in current, similar to how a spring resists changes in its length. The faster you try to change the current (higher frequency), the more the inductor opposes it.
3. Capacitor (C)
The capacitor stores energy in an electric field and allows current to flow when the voltage across it changes. The capacitive reactance () is also frequency-dependent and is given by the formula:
![\[ X_C = \frac{1}{2\pi f C} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-1ad2c6c83752439fe0d271c3d3ec2625_l3.png "Rendered by QuickLaTeX.com")
Where:
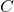is the capacitance in farads (F).- Illustrative Explanation: Think of a capacitor as a water tank that fills and empties. When the voltage changes, the capacitor allows current to flow in or out, similar to how water flows in and out of a tank based on the water level.
Calculating Impedance in a Series LCR Circuit
To calculate the total impedance (
) in a series LCR circuit, we need to consider the contributions of resistance and reactance. The total reactance () is the difference between inductive reactance and capacitive reactance:
![\[ X = X_L - X_C \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ced8cd09ee332fa6054a5e302972ce9b_l3.png "Rendered by QuickLaTeX.com")
Thus, the total impedance can be expressed as:
![\[ Z = R + j(X_L - X_C) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-fe5eea73ce561b04e8ed841cfa4c3c5d_l3.png "Rendered by QuickLaTeX.com")
Magnitude of Impedance
The magnitude of the impedance can be calculated using the formula:
![\[ |Z| = \sqrt{R^2 + (X_L - X_C)^2} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ca6e430c8c91c3490a02a7e10d195273_l3.png "Rendered by QuickLaTeX.com")
Phase Angle
The phase angle (
) between the voltage and current in the circuit can be determined using:
![\[ \tan(\phi) = \frac{X_L - X_C}{R} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-0a733c872a81002b0bef0071a3efeede_l3.png "Rendered by QuickLaTeX.com")
- Illustrative Explanation: Imagine a seesaw. The resistance (R) is one side, while the difference between inductive and capacitive reactance (
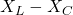) is the other side. The seesaw’s balance point (the phase angle) indicates how the current and voltage are related in the circuit.
Significance of Impedance in Series LCR Circuits
1. Resonance
In a series LCR circuit, resonance occurs when the inductive reactance equals the capacitive reactance (
). At this point, the total impedance is minimized, and the circuit can draw maximum current from the source. The resonant frequency (
) can be calculated using:
![\[ f_0 = \frac{1}{2\pi\sqrt{LC}} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-c0de53bfb90f7fc665794150eed6a707_l3.png "Rendered by QuickLaTeX.com")
- Illustrative Explanation: Think of a swing at a playground. When you push the swing at just the right moment (the resonant frequency), it goes higher and higher. Similarly, at resonance, the circuit can draw maximum energy from the source.
2. Power Factor
The power factor (PF) is a measure of how effectively the circuit converts electrical power into useful work. It is defined as the cosine of the phase angle:
![\[ \text{PF} = \cos(\phi) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-57aa65dbf0ff3b83f7439e9f645857fb_l3.png "Rendered by QuickLaTeX.com")
A power factor of 1 indicates that all the power is being used effectively, while a power factor less than 1 indicates that some power is reactive and not doing useful work.
- Illustrative Explanation: Imagine a car engine. A power factor of 1 is like an engine running at peak efficiency, converting all fuel into motion. A lower power factor indicates wasted energy, similar to an engine that is idling or running inefficiently.
3. Impedance Matching
In many applications, such as audio systems and radio transmitters, impedance matching is crucial for maximizing power transfer between components. By ensuring that the impedance of the source matches the impedance of the load, engineers can minimize reflections and losses.
- Illustrative Explanation: Think of a water hose connected to a sprinkler. If the hose diameter matches the sprinkler’s inlet, water flows smoothly. If the diameters are mismatched, water may spray inefficiently or not at all, similar to how impedance matching ensures efficient power transfer.
Applications of Series LCR Circuits
1. Filters
Series LCR circuits are commonly used in filter applications, such as low-pass, high-pass, band-pass, and band-stop filters. By selecting appropriate values for R, L, and C, engineers can design circuits that allow certain frequencies to pass while attenuating others.
- Illustrative Explanation: Imagine a sieve used to separate different sizes of grains. Just as the sieve allows smaller grains to pass through while blocking larger ones, LCR circuits can filter out unwanted frequencies.
2. Tuning Circuits
In radio and television receivers, series LCR circuits are used as tuning circuits to select specific frequencies from a range of signals. By adjusting the values of L and C, the circuit can be tuned to resonate at the desired frequency.
- Illustrative Explanation: Think of a radio dial. Just as turning the dial allows you to tune into different stations, adjusting the L and C values in a tuning circuit allows you to select specific frequencies.
3. Oscillators
Series LCR circuits are also used in oscillator circuits, which generate continuous waveforms at specific frequencies. These circuits are essential in applications such as clock generation, signal modulation, and waveform generation.
- Illustrative Explanation: Imagine a pendulum swinging back and forth. Just as the pendulum creates a rhythmic motion, an LCR circuit can generate oscillating signals, producing consistent waveforms for various applications.
Conclusion
Impedance in series LCR circuits is a fundamental concept that combines resistance and reactance to describe the total opposition to alternating current. By understanding its definition, characteristics, calculations, and significance, we can appreciate the role of impedance in various applications, from filtering and tuning to oscillation. Whether designing audio systems, radio receivers, or electronic devices, the principles of impedance continue to shape our understanding of AC circuits and their behavior. As we navigate the complexities of electrical engineering, the concept of impedance serves as a vital tool for innovation and design, ensuring that our systems operate efficiently and effectively.