The interference of waves is a fundamental phenomenon in physics that occurs when two or more waves overlap and combine to form a new wave pattern. This concept is crucial in various fields, including acoustics, optics, and quantum mechanics. This article will provide an in-depth examination of wave interference, covering its definition, types, mathematical descriptions, examples, and applications, along with illustrative explanations to enhance understanding.
1. Definition of Wave Interference
Wave interference is defined as the process by which two or more waves superimpose to form a resultant wave. This interaction can lead to various outcomes depending on the phase relationship between the waves involved. When waves meet, they can either reinforce each other, leading to increased amplitude, or cancel each other out, resulting in reduced amplitude. The resulting wave pattern is determined by the principle of superposition, which states that the total displacement at any point is the sum of the displacements of the individual waves.
Illustrative Explanation: Imagine two people jumping on a trampoline at the same time. If they jump in sync (at the same time and height), they create a larger bounce together, similar to constructive interference. However, if one person jumps while the other is coming down, they may cancel each other out, resulting in a smaller bounce, akin to destructive interference.
2. Types of Wave Interference
Wave interference can be categorized into two primary types: constructive interference and destructive interference.
- Constructive Interference: This occurs when two waves meet in phase, meaning their crests and troughs align. When this happens, the amplitudes of the waves add together, resulting in a wave with a greater amplitude. The mathematical representation of constructive interference can be expressed as:
![]()
Where ![]() is the amplitude of the resultant wave, and
is the amplitude of the resultant wave, and ![]() and
and ![]() are the amplitudes of the individual waves.
are the amplitudes of the individual waves.
Illustrative Explanation: Consider two sound waves produced by two speakers playing the same note. If the speakers are positioned such that the sound waves from both speakers reach a listener’s ear at the same time and in phase, the sound will be louder than if only one speaker were playing. This is because the sound waves constructively interfere, amplifying the sound.
- Destructive Interference: This occurs when two waves meet out of phase, meaning the crest of one wave aligns with the trough of another. In this case, the amplitudes partially or completely cancel each other out, resulting in a wave with a smaller amplitude or no wave at all. The mathematical representation of destructive interference can be expressed as:
![]()
Where ![]() is the amplitude of the wave that is in phase with the crest, and
is the amplitude of the wave that is in phase with the crest, and ![]() is the amplitude of the wave that is in phase with the trough.
is the amplitude of the wave that is in phase with the trough.
Illustrative Explanation: Imagine two people singing the same note but one is slightly off-key. If they sing together, the sound may become quieter or even inaudible at certain points due to destructive interference, where the sound waves cancel each other out.
3. Mathematical Description of Wave Interference
The mathematical analysis of wave interference often involves the use of trigonometric functions to describe the waves. For two waves traveling in the same medium, the general form of the waves can be expressed as:
![]()
![]()
Where:
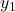 and
and 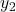 are the displacements of the two waves.
are the displacements of the two waves.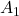 and
and 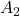 are the amplitudes of the waves.
are the amplitudes of the waves.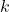 is the wave number, related to the wavelength.
is the wave number, related to the wavelength.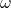 is the angular frequency, related to the frequency of the waves.
is the angular frequency, related to the frequency of the waves.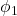 and
and 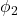 are the phase constants of the waves.
are the phase constants of the waves.
The resultant wave ![]() can be expressed as:
can be expressed as:
![]()
Using the principle of superposition, the resultant wave can be analyzed to determine whether the interference is constructive or destructive based on the phase difference between the two waves.
Illustrative Explanation: To visualize this, consider two waves represented on a graph. If both waves have the same amplitude and frequency but are perfectly in phase, their peaks align, and the resultant wave will have double the amplitude. Conversely, if one wave is shifted by half a wavelength (180 degrees out of phase), the peaks of one wave will align with the troughs of the other, resulting in a flat line (no wave).
4. Examples of Wave Interference
Wave interference is a common phenomenon observed in various contexts. Here are a few illustrative examples:
- Water Waves: When two stones are thrown into a pond at the same time, the ripples created by each stone will overlap. Depending on the timing and position of the stones, the resulting wave pattern can show areas of increased wave height (constructive interference) and areas where the waves cancel each other out (destructive interference).
- Sound Waves: In a concert hall, the sound waves produced by multiple instruments can interfere with each other. If two instruments play the same note in perfect harmony, the sound will be amplified due to constructive interference. However, if one instrument is slightly out of tune, the sound may become muddled or quieter due to destructive interference.
- Light Waves: The famous double-slit experiment demonstrates wave interference with light. When coherent light (light of a single wavelength) passes through two closely spaced slits, it creates an interference pattern on a screen. Bright and dark fringes appear due to constructive and destructive interference, respectively, illustrating the wave nature of light.
Illustrative Explanation: In the double-slit experiment, imagine shining a flashlight through two narrow openings. Instead of just two bright spots on the wall, you see a series of alternating bright and dark bands. The bright bands correspond to points where the light waves from the two slits constructively interfere, while the dark bands correspond to points where they destructively interfere.
5. Applications of Wave Interference
Wave interference has numerous practical applications across various fields:
- Acoustics: Understanding interference is crucial in designing concert halls and auditoriums. Architects use principles of wave interference to enhance sound quality, ensuring that sound waves from different sources combine constructively in the audience area.
- Optics: Interference is fundamental in optical devices such as interferometers, which are used to measure small distances, changes in refractive index, and surface irregularities. These devices exploit the interference of light waves to produce precise measurements.
- Telecommunications: In wireless communication, interference can affect signal quality. Engineers design systems to minimize destructive interference and enhance constructive interference, ensuring clear transmission of information.
- Noise-Canceling Headphones: These devices use destructive interference to reduce unwanted ambient sounds. By generating sound waves that are out of phase with the incoming noise, they effectively cancel out the sound, providing a quieter listening experience.
Illustrative Explanation: Consider a concert hall designed with curved walls. The shape of the walls helps direct sound waves toward the audience, ensuring that the sound from the stage reaches everyone clearly. This design takes advantage of constructive interference, allowing the audience to experience a rich and full sound.
Conclusion
The interference of waves is a fundamental concept that plays a critical role in understanding various physical phenomena. By exploring the definitions, types, mathematical descriptions, examples, and applications of wave interference, we gain a deeper appreciation for its significance in both natural and technological contexts. From the ripples in a pond to the intricate patterns of light and sound, wave interference is a powerful demonstration of the principles of superposition and the wave nature of energy. As we continue to study and apply these principles, we unlock new possibilities for innovation and understanding in the world around us.