The inverse cosine function, denoted as ![]() or
or ![]() , is a fundamental concept in trigonometry that allows us to determine the angle whose cosine is a given value. This function is essential in various fields, including mathematics, physics, engineering, and computer science, as it provides a means to solve problems involving angles and their relationships to the sides of triangles. This article aims to provide an exhaustive overview of the inverse cosine function, detailing its definition, properties, graphical representation, applications, and illustrative explanations for each concept.
, is a fundamental concept in trigonometry that allows us to determine the angle whose cosine is a given value. This function is essential in various fields, including mathematics, physics, engineering, and computer science, as it provides a means to solve problems involving angles and their relationships to the sides of triangles. This article aims to provide an exhaustive overview of the inverse cosine function, detailing its definition, properties, graphical representation, applications, and illustrative explanations for each concept.
1. Definition of Inverse Cosine
The inverse cosine function is defined as the function that returns the angle ![]() for which the cosine is equal to a given value
for which the cosine is equal to a given value ![]() . Mathematically, this can be expressed as:
. Mathematically, this can be expressed as:
![]()
The range of the inverse cosine function is restricted to ensure that it is a well-defined function. Specifically, the range of ![]() is:
is:
![]()
This means that the inverse cosine function will return angles in the first and second quadrants of the unit circle.
- Illustrative Explanation: If you know that the cosine of an angle is
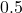 , you can use the inverse cosine function to find the angle. Specifically,
, you can use the inverse cosine function to find the angle. Specifically, 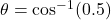 yields
yields 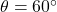 (or
(or 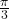 radians) because
radians) because 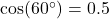 .
.
2. Properties of Inverse Cosine
The inverse cosine function has several important properties that are useful in various mathematical contexts:
2.1. Domain and Range
The domain of the inverse cosine function is restricted to the interval ![]() , meaning that it can only accept values within this range. The corresponding range, as mentioned earlier, is
, meaning that it can only accept values within this range. The corresponding range, as mentioned earlier, is ![]() .
.
- Illustrative Explanation: If you attempt to calculate
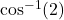 or
or 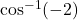 , you will find that these values are undefined because the cosine of an angle cannot exceed
, you will find that these values are undefined because the cosine of an angle cannot exceed 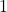 or be less than
or be less than 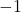 .
.
2.2. Even Function Property
The inverse cosine function is an even function, which means that:
![]()
This property reflects the symmetry of the cosine function about the y-axis.
- Illustrative Explanation: If you know that
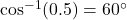 , then using the even function property, you can find
, then using the even function property, you can find 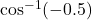 :
:
![]()
2.3. Relationship with Cosine
The inverse cosine function is directly related to the cosine function. Specifically, if ![]() , then:
, then:
![]()
This relationship is fundamental in solving trigonometric equations.
- Illustrative Explanation: If you find that
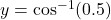 gives you
gives you 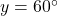 , you can confirm this by checking that
, you can confirm this by checking that 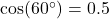 .
.
2.4. Derivative of Inverse Cosine
The derivative of the inverse cosine function can be expressed as:
![]()
This derivative is useful in calculus, particularly in optimization problems and when dealing with integrals involving inverse trigonometric functions.
- Illustrative Explanation: If you want to find the rate of change of the angle with respect to the cosine value, you can use this derivative. For example, if
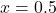 , the derivative at this point would be:
, the derivative at this point would be:
![]()
This indicates that as the cosine value increases, the angle decreases at this rate.
3. Graphical Representation of Inverse Cosine
The graphical representation of the inverse cosine function provides a visual understanding of how the function behaves across its domain.
3.1. Graph Characteristics
The graph of the inverse cosine function is a decreasing curve that starts at ![]() and ends at
and ends at ![]() . The function is continuous and smooth, reflecting the fact that it is a well-defined function over its domain.
. The function is continuous and smooth, reflecting the fact that it is a well-defined function over its domain.
- Illustrative Explanation: If you were to plot the function, you would see that as
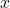 moves from
moves from 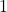 to
to 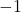 , the angle
, the angle 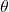 decreases from
decreases from 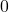 to
to 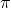 . For example, at
. For example, at 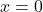 ,
, 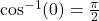 (or
(or 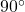 ).
).
3.2. Example Points on the Graph
To illustrate the behavior of the inverse cosine function, consider the following points:
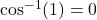
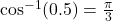 (or
(or 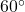 )
)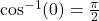 (or
(or 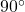 )
)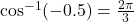 (or
(or 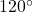 )
)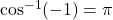 (or
(or 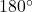 )
)
These points can be plotted to visualize the decreasing nature of the function.
4. Applications of Inverse Cosine
The inverse cosine function has various applications across different fields:
4.1. Geometry
In geometry, the inverse cosine function is used to find angles in triangles when the lengths of the sides are known. This is particularly useful in solving problems involving the Law of Cosines.
- Illustrative Explanation: If you have a triangle with sides of lengths
 ,
, 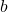 , and
, and  , you can find the angle opposite side
, you can find the angle opposite side  using the formula:
using the formula:
![]()
Then, to find angle ![]() , you would use
, you would use ![]() .
.
4.2. Physics
In physics, the inverse cosine function is used in problems involving vectors, particularly when calculating angles between forces or velocities.
- Illustrative Explanation: If you have two vectors and you want to find the angle between them, you can use the dot product formula:
![Rendered by QuickLaTeX.com \[ \cos(\theta) = \frac{\vec{A} \cdot \vec{B}}{|\vec{A}| |\vec{B}|} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f8b1d4018e9bbfd0e1d3e92d4e47b69e_l3.png)
Then, to find the angle ![]() , you would use
, you would use ![]() .
.
4.3. Engineering
In engineering, the inverse cosine function is used in various applications, including signal processing, control systems, and structural analysis.
- Illustrative Explanation: When analyzing the stability of structures, engineers may need to calculate angles of forces acting on beams or trusses, using the inverse cosine function to determine the angles based on the forces involved.
4.4. Computer Graphics
In computer graphics, the inverse cosine function is used to calculate angles for rendering 3D objects and animations, particularly in lighting and shading calculations.
- Illustrative Explanation: When determining the angle of incidence of light on a surface, the inverse cosine function can help calculate the angle based on the normal vector and the light source direction.
Conclusion
In conclusion, the inverse cosine function is a fundamental mathematical concept that allows us to determine angles based on cosine values. It has several important properties, including its domain and range, even function property, and relationship with the cosine function. The graphical representation of the inverse cosine function provides a visual understanding of its behavior, while its applications span various fields, including geometry, physics, engineering, and computer graphics. By understanding the inverse cosine function and its properties, we gain valuable insights into its relevance in mathematical analysis and real-world applications. As we continue to explore mathematics and its applications, the knowledge of the inverse cosine function will remain a key component of our mathematical toolkit.