Kepler’s Laws of Planetary Motion: An In-Depth Exploration

Kepler’s Laws of Planetary Motion are three fundamental principles that describe the motion of planets around the Sun. Formulated by the German astronomer Johannes Kepler in the early 17th century, these laws were pivotal in the development of celestial mechanics and laid the groundwork for Newton’s law of universal gravitation. This comprehensive article will delve into each of Kepler’s three laws, providing detailed explanations, illustrative examples, and their significance in the field of astronomy.

Overview of Kepler’s Laws

Kepler’s Laws can be summarized as follows:

1. Kepler’s First Law (Law of Ellipses): The orbit of a planet around the Sun is an ellipse, with the Sun at one of the two foci.
2. Kepler’s Second Law (Law of Equal Areas): A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
3. Kepler’s Third Law (Law of Harmonies): The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.

Kepler’s First Law: Law of Ellipses

Statement: The orbit of a planet around the Sun is an ellipse, with the Sun located at one of the two foci of the ellipse.

Illustrative Explanation: To visualize this law, imagine a stretched rubber band that forms an oval shape when released. This oval shape is an ellipse. In the context of planetary motion, the Sun is positioned at one focus of the ellipse, while the other focus remains empty.

Key Features of an Ellipse:
Foci: An ellipse has two focal points. In the case of planetary orbits, one focus is occupied by the Sun, while the other is a point in space with no physical object.
Major and Minor Axes: The longest diameter of the ellipse is called the major axis, while the shortest diameter is the minor axis. The semi-major axis is half the length of the major axis and is a crucial parameter in defining the size of the orbit.

Significance: Kepler’s First Law challenged the long-held belief that planetary orbits were circular. It provided a more accurate description of the paths that planets follow, which are elliptical in shape, leading to a better understanding of their motion.

Kepler’s Second Law: Law of Equal Areas

Statement: A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.

Illustrative Explanation: Imagine a planet moving along its elliptical orbit. As it travels, if you draw an imaginary line from the planet to the Sun, this line will sweep out an area. According to Kepler’s Second Law, if you measure the area swept out by this line over a specific time interval, it will be the same regardless of where the planet is in its orbit.

Variable Speed: This law implies that a planet moves faster when it is closer to the Sun (at perihelion) and slower when it is farther from the Sun (at aphelion). For example, when Earth is closest to the Sun in early January, it moves faster in its orbit than when it is farthest from the Sun in early July.

Mathematical Representation: If $A$ is the area swept out by the line segment in time $t$ , then:

$\frac{A_1}{t_1} = \frac{A_2}{t_2}$

This means that the ratio of the area to the time interval is constant.

Significance: Kepler’s Second Law highlights the conservation of angular momentum in planetary motion. It explains why planets do not move at a constant speed in their orbits and provides insight into the dynamics of celestial bodies.

Kepler’s Third Law: Law of Harmonies

Statement: The square of the orbital period of a planet (the time it takes to complete one full orbit around the Sun) is directly proportional to the cube of the semi-major axis of its orbit.

Mathematical Representation: This law can be expressed mathematically as:

$T^2 \propto a^3$

Where:

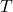$T$ is the orbital period of the planet (in years).
$a$ is the semi-major axis of the orbit (in astronomical units, AU).

Illustrative Explanation: To understand this law, consider two planets in our solar system: Earth and Mars. Earth has an orbital period of 1 year and a semi-major axis of 1 AU. Mars, on the other hand, has a semi-major axis of about 1.52 AU. According to Kepler’s Third Law, we can calculate the relationship between their orbital periods.

For Earth:

$T_E^2 = 1^2 = 1$

For Mars:

$T_M^2 = (1.52)^3 \approx 3.51$

Thus, Mars takes longer to orbit the Sun than Earth, which aligns with our observations.

Significance: Kepler’s Third Law provides a powerful tool for comparing the orbits of different planets. It allows astronomers to predict the orbital periods of planets based on their distances from the Sun, reinforcing the understanding of gravitational interactions in the solar system.

Applications and Implications of Kepler’s Laws

1. Celestial Mechanics: Kepler’s Laws are foundational in celestial mechanics, allowing astronomers to calculate the positions and motions of celestial bodies. They are essential for predicting the orbits of satellites, comets, and other celestial objects.

2. Space Exploration: Understanding Kepler’s Laws is crucial for planning space missions. For example, when sending spacecraft to other planets, mission planners must account for the elliptical orbits of both the spacecraft and the target planet to ensure successful rendezvous.

3. Gravitational Theory: Kepler’s Laws laid the groundwork for Isaac Newton’s law of universal gravitation. Newton’s work provided a theoretical framework that explained why planets follow the paths described by Kepler’s Laws, linking the motion of celestial bodies to gravitational forces.

4. Astrophysics: Kepler’s Laws are used in astrophysics to study the dynamics of star systems, galaxies, and the universe as a whole. They help scientists understand the behavior of objects in gravitational fields and the formation of planetary systems.

Conclusion

In conclusion, Kepler’s Laws of Planetary Motion are fundamental principles that describe the motion of planets around the Sun. Kepler’s First Law reveals the elliptical nature of orbits, the Second Law illustrates the variable speeds of planets, and the Third Law establishes a relationship between orbital periods and distances from the Sun. Together, these laws provide a comprehensive framework for understanding celestial motion and have had a profound impact on the fields of astronomy, physics, and space exploration. By studying Kepler’s Laws, we gain valuable insights into the dynamics of our solar system and the fundamental forces that govern the motion of celestial bodies. As we continue to explore the universe, Kepler’s Laws remain a cornerstone of our understanding of planetary motion and the intricate dance of the cosmos.

Blog.Pengayaan.Com