Uniformly accelerated motion is a fundamental concept in physics that describes the motion of an object that is experiencing a constant acceleration. This type of motion is prevalent in various real-world scenarios, from vehicles accelerating on a highway to objects falling under the influence of gravity. This extensive article will delve into the definition of uniformly accelerated motion, its key characteristics, the equations of motion, graphical representations, examples in everyday life, and its significance in the study of physics, providing illustrative explanations for each concept.
Definition of Uniformly Accelerated Motion
Uniformly accelerated motion refers to the motion of an object in which its velocity changes at a constant rate over time. This means that the acceleration remains constant, leading to a linear relationship between the displacement of the object and the time elapsed.
Illustrative Explanation: Imagine a car accelerating from a stoplight. If the car increases its speed at a steady rate, such as 5 meters per second every second, it is undergoing uniformly accelerated motion. Just as the car’s speed increases consistently, the object’s velocity changes uniformly over time.
Key Characteristics of Uniformly Accelerated Motion
1. Constant Acceleration: In uniformly accelerated motion, the acceleration remains constant throughout the motion. This means that the rate of change of velocity is the same at all points in time.
Illustrative Explanation: Think of a sprinter running on a track. If the sprinter increases their speed by the same amount every second, they are experiencing constant acceleration. Just as the sprinter maintains a steady increase in speed, the object in uniformly accelerated motion maintains a constant acceleration.
2. Linear Velocity-Time Relationship: The velocity of an object undergoing uniformly accelerated motion changes linearly with time. This means that if you were to plot velocity against time, the graph would be a straight line.
Illustrative Explanation: Picture a staircase. Just as each step represents a consistent increase in height, each point on the velocity-time graph represents a consistent increase in velocity over time.
3. Quadratic Displacement-Time Relationship: The displacement of an object undergoing uniformly accelerated motion changes quadratically with time. This means that if you were to plot displacement against time, the graph would be a parabola.
Illustrative Explanation: Imagine throwing a ball into the air. As the ball rises, it covers more distance in each successive second. Just as the distance increases more rapidly as the ball moves upward, the displacement-time graph for uniformly accelerated motion forms a curve.
Equations of Motion
The equations of motion for uniformly accelerated motion are derived from the relationships between displacement, velocity, acceleration, and time. The three primary equations are:
1. First Equation of Motion:
![\[ v = u + at \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-a4bbe9a22197edd7a53649794e57731a_l3.png "Rendered by QuickLaTeX.com")
where:
= final velocity
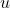= initial velocity
= acceleration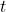
= time
Illustrative Explanation: Think of a runner starting a race. If the runner begins at a certain speed (initial velocity) and accelerates at a constant rate, the final speed after a certain time can be calculated using this equation. Just as the runner’s speed increases over time, the equation shows how velocity changes with acceleration.
2. Second Equation of Motion:
![\[ s = ut + \frac{1}{2}at^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-956d5e2bc9705ff9ab425504deee779c_l3.png "Rendered by QuickLaTeX.com")
where:
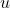= displacement- = initial velocity
- = acceleration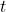
- = time
Illustrative Explanation: Imagine a car that starts moving from rest. The distance it travels over time can be calculated using this equation. Just as the car covers more ground as it accelerates, the equation accounts for both the initial speed and the effect of acceleration on displacement.
3. Third Equation of Motion:
![\[ v^2 = u^2 + 2as \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-1bc3e62b915210541fb0882da789d0c3_l3.png "Rendered by QuickLaTeX.com")
where:
- = final velocity
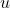- = initial velocity
- = acceleration
- = displacement
Illustrative Explanation: Think of a skateboarder pushing off the ground. The final speed of the skateboarder can be determined using this equation, which relates the change in speed to the distance traveled and the acceleration. Just as the skateboarder gains speed as they travel, the equation shows how velocity is influenced by displacement and acceleration.
Graphical Representations
Graphical representations are essential for visualizing uniformly accelerated motion. The two primary graphs used are the velocity-time graph and the displacement-time graph.
1. Velocity-Time Graph: In a velocity-time graph for uniformly accelerated motion, the slope of the line represents acceleration. A straight line indicates constant acceleration, while the area under the line represents displacement.
Illustrative Explanation: Imagine a ramp leading up to a platform. Just as the ramp has a consistent incline, the straight line on the velocity-time graph indicates a constant increase in speed. The steeper the line, the greater the acceleration.
2. Displacement-Time Graph: In a displacement-time graph for uniformly accelerated motion, the curve represents the changing displacement over time. The slope of the curve indicates velocity, and the curvature indicates acceleration.
Illustrative Explanation: Picture a roller coaster ride. Just as the coaster moves faster as it descends, the curve on the displacement-time graph shows how distance increases more rapidly over time as the object accelerates.
Examples of Uniformly Accelerated Motion
Uniformly accelerated motion can be observed in various real-world scenarios:
1. Free Fall: An object falling freely under the influence of gravity experiences uniformly accelerated motion. The acceleration due to gravity is approximately 
, and the object’s velocity increases as it falls.
Illustrative Explanation: Think of a dropped ball. Just as the ball picks up speed as it falls, it undergoes uniformly accelerated motion due to the constant acceleration of gravity.
2. Vehicles Accelerating: When a car accelerates from a stoplight at a constant rate, it is undergoing uniformly accelerated motion. The car’s speed increases steadily over time until it reaches a desired velocity.
Illustrative Explanation: Imagine a car at a traffic light. Just as the driver presses the gas pedal to increase speed steadily, the car experiences uniformly accelerated motion as it moves forward.
3. Projectile Motion: When an object is thrown upward, it experiences uniformly accelerated motion both on the way up and on the way down. The object decelerates as it rises and accelerates as it falls back down.
Illustrative Explanation: Picture a basketball thrown into the air. Just as the ball slows down as it rises and speeds up as it falls, it undergoes uniformly accelerated motion influenced by gravity.
Significance of Uniformly Accelerated Motion
Understanding uniformly accelerated motion is significant for several reasons:
1. Foundation of Kinematics: Uniformly accelerated motion is a fundamental concept in kinematics, the branch of physics that deals with the motion of objects. It provides a basis for understanding more complex motion scenarios.
Illustrative Explanation: Think of uniformly accelerated motion as the building blocks of a structure. Just as a solid foundation supports a building, understanding this concept supports the study of more advanced topics in physics.
2. Real-World Applications: The principles of uniformly accelerated motion are applied in various fields, including engineering, automotive design, and sports science. Understanding how objects accelerate helps engineers design safer vehicles and optimize performance.
Illustrative Explanation: Imagine an engineer designing a roller coaster. Just as the engineer must consider how the coaster will accelerate and decelerate, understanding uniformly accelerated motion is crucial for creating safe and thrilling rides.
3. Predictive Modeling: The equations of motion for uniformly accelerated motion allow scientists and engineers to predict the behavior of moving objects. This predictive capability is essential for designing systems and understanding natural phenomena.
Illustrative Explanation: Think of a weather forecaster predicting a storm. Just as the forecaster uses data to make predictions, scientists use the equations of uniformly accelerated motion to predict how objects will move under various conditions.
Conclusion
In conclusion, uniformly accelerated motion is a fundamental concept in physics characterized by constant acceleration, linear velocity-time relationships, and quadratic displacement-time relationships. The equations of motion, graphical representations, and real-world examples illustrate the significance of this concept in understanding the behavior of moving objects. By grasping the principles of uniformly accelerated motion, we can apply this knowledge to various fields, from engineering to sports science, and enhance our understanding of the physical world. As we continue to explore the intricacies of motion, uniformly accelerated motion remains a cornerstone of kinematics, providing valuable insights into the dynamics of objects in motion. Through ongoing research and education, we can deepen our understanding of this essential concept and its applications, ensuring that we utilize its principles for the benefit of science and society as a whole.