Linear Momentum: A Comprehensive Exploration

Linear momentum is a fundamental concept in physics that describes the quantity of motion an object possesses. It plays a crucial role in understanding the behavior of moving objects and is a key principle in mechanics. This article will delve into the definition of linear momentum, its properties, the principle of conservation of momentum, mathematical representation, examples, applications, and its significance in various fields, providing illustrative explanations for each concept.

Definition of Linear Momentum

Linear momentum, often simply referred to as momentum, is defined as the product of an object’s mass and its velocity. It is a vector quantity, meaning it has both magnitude and direction. The formula for linear momentum () is given by:

   

Where:

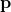• is the linear momentum.
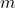• is the mass of the object.
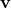• is the velocity of the object.

Illustrative Explanation

Imagine a bowling ball rolling down a lane. The momentum of the bowling ball depends on how heavy it is (its mass) and how fast it is moving (its velocity). If you were to roll a lighter ball at the same speed, it would have less momentum than the heavier bowling ball. This illustrates how both mass and velocity contribute to the overall momentum of an object.

Properties of Linear Momentum

Linear momentum has several key properties that define its behavior:

1. Direction: The direction of linear momentum is the same as the direction of the object’s velocity. If an object is moving to the right, its momentum is also directed to the right.

Illustrative Explanation

Think of a car driving down a straight road. If the car is moving forward, its momentum is also directed forward. If the car suddenly turns left, its momentum changes direction accordingly.

2. Conservation: In a closed system with no external forces acting on it, the total linear momentum remains constant. This principle is known as the conservation of momentum.

Illustrative Explanation

Imagine two ice skaters pushing off each other on a frictionless ice rink. When they push away from each other, the momentum they gain in opposite directions is equal and opposite, resulting in no change in the total momentum of the system.

3. Dependence on Mass and Velocity: Linear momentum is directly proportional to both the mass and velocity of an object. Doubling either the mass or the velocity will double the momentum.

Illustrative Explanation

Consider a truck and a bicycle moving at the same speed. The truck, being much heavier, has significantly more momentum than the bicycle. If both the truck and the bicycle were to double their speeds, their momenta would also double, but the truck would still have much more momentum than the bicycle.

The Principle of Conservation of Momentum

The principle of conservation of momentum states that in an isolated system (one with no external forces), the total momentum before an event (such as a collision) is equal to the total momentum after the event. This principle is fundamental in analyzing collisions and interactions between objects.

Illustrative Explanation

Imagine two billiard balls colliding on a pool table. Before the collision, the first ball has a certain momentum, and the second ball has another momentum. After they collide, the total momentum of both balls combined remains the same, even though they may change direction and speed. This conservation allows players to predict the outcome of the collision based on the initial momenta.

Mathematical Representation of Linear Momentum

The mathematical representation of linear momentum can be expressed as:

   

Where:

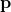• is the linear momentum vector.
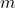• is the mass of the object.
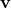• is the velocity vector.

Illustrative Explanation

Consider a soccer ball with a mass of 0.5 kg moving at a velocity of 10 m/s. The momentum of the soccer ball can be calculated as:

   

This means the soccer ball has a momentum of 5 kg m/s in the direction it is moving.

Examples of Linear Momentum

Linear momentum can be observed in various real-world scenarios:

1. Collisions: When two cars collide, the total momentum before the collision is equal to the total momentum after the collision, assuming no external forces act on them.

Illustrative Explanation

Imagine two cars approaching each other at an intersection. When they collide, the momentum they had before the collision is transferred between them, affecting their speeds and directions after the impact.

2. Sports: In sports like football or basketball, players use their momentum to tackle opponents or make shots. The momentum of a player can influence the outcome of a play.

Illustrative Explanation

Think of a football player running toward the end zone. The faster and heavier the player, the more momentum they have, making it harder for defenders to stop them.

3. Rocket Propulsion: Rockets operate on the principle of conservation of momentum. As they expel gas downward, they gain momentum in the opposite direction, propelling them upward.

Illustrative Explanation

Picture a balloon filled with air. When you release the balloon without tying it, the air rushes out one end, and the balloon flies off in the opposite direction. This is similar to how rockets work, using the conservation of momentum to propel themselves into space.

Applications of Linear Momentum

Linear momentum has numerous applications across various fields:

1. Engineering: Engineers use the principles of linear momentum to design safe vehicles, structures, and machinery. Understanding how momentum affects collisions helps in creating safer designs.

Illustrative Explanation

In car design, engineers analyze how the momentum of a vehicle changes during a crash to improve safety features like crumple zones and airbags, which absorb momentum and reduce injury.

2. Sports Science: Coaches and athletes analyze momentum to improve performance in sports. Understanding how to maximize momentum can lead to better techniques and strategies.

Illustrative Explanation

In track and field, sprinters learn to optimize their speed and momentum during a race to achieve faster times. Coaches may use video analysis to help athletes understand their momentum during different phases of a race.

3. Astrophysics: The conservation of momentum is crucial in understanding celestial mechanics, such as the motion of planets, stars, and galaxies. It helps scientists predict the behavior of astronomical bodies.

Illustrative Explanation

Consider two stars in a binary system orbiting each other. The momentum of the two stars is conserved as they move through space, allowing astronomers to calculate their masses and distances based on their orbital motions.

Significance of Linear Momentum

Linear momentum is significant in understanding the dynamics of motion and the interactions between objects. It provides insights into how forces affect motion and is a foundational concept in classical mechanics. By studying linear momentum, scientists and engineers can develop better technologies, improve safety, and enhance our understanding of the natural world.

Illustrative Explanation

Think of linear momentum as a fundamental building block of motion. Just as bricks are used to construct a sturdy wall, linear momentum helps us understand how objects move and interact in our universe. Whether it’s a car on the road, a player on the field, or a rocket in space, momentum is a key factor in determining how they behave.

Conclusion

In conclusion, linear momentum is a fundamental concept in physics characterized by the product of an object’s mass and its velocity. Understanding the properties, the principle of conservation of momentum, mathematical representation, examples, applications, and significance of linear momentum is essential for grasping various physical phenomena. From collisions to sports and astrophysics, linear momentum plays a vital role in our understanding of motion and interactions between objects. By appreciating the intricacies of linear momentum, we can better navigate its implications in both scientific and practical contexts.