The azimuthal quantum number, often denoted as 
, is a fundamental concept in quantum mechanics that describes the shape of atomic orbitals and the angular momentum of electrons in an atom. It plays a crucial role in determining the energy levels and spatial distribution of electrons around the nucleus. This article will provide a detailed exploration of the azimuthal quantum number, including its definition, significance, relationship with other quantum numbers, and illustrative explanations to enhance understanding.
1. Definition of the Azimuthal Quantum Number
The azimuthal quantum number is one of the four quantum numbers used to describe the unique quantum state of an electron in an atom. It specifically indicates the subshell or orbital shape in which an electron resides. The azimuthal quantum number can take on integer values ranging from 
to 
, where 
is the principal quantum number that denotes the energy level of the electron.
Illustrative Explanation: Imagine a set of nested spheres representing different energy levels in an atom. The azimuthal quantum number determines the shape of these spheres. For example, if 
, the possible values of are 
and 
, corresponding to different shapes of orbitals within that energy level.
2. Significance of the Azimuthal Quantum Number
The azimuthal quantum number is significant for several reasons:
A. Determining Orbital Shapes
The value of the azimuthal quantum number directly influences the shape of the electron’s orbital. Each value of corresponds to a specific type of orbital:
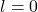: s orbital (spherical shape)
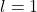: p orbital (dumbbell shape)
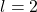: d orbital (cloverleaf shape)
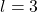: f orbital (complex shapes)
Illustrative Explanation: Picture a balloon (s orbital) that is perfectly round. Now, imagine stretching that balloon into a figure-eight shape (p orbital). As you increase the complexity, you can visualize the cloverleaf shape of a d orbital. Each shape represents the probability distribution of finding an electron in that orbital.
B. Angular Momentum of Electrons
The azimuthal quantum number is also related to the angular momentum of an electron in an atom. The angular momentum 
can be calculated using the formula:
![\[ L = \sqrt{l(l + 1)} \hbar \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-7b68a27c4d5dd32e6a61c614c6b40d6b_l3.png "Rendered by QuickLaTeX.com")
where 
is the reduced Planck’s constant. This relationship shows that higher values of correspond to greater angular momentum.
Illustrative Explanation: Imagine a spinning top. The faster it spins, the more angular momentum it has. Similarly, electrons with higher azimuthal quantum numbers (higher values) have greater angular momentum, which affects their behavior in an atom.
C. Energy Level Splitting
In multi-electron atoms, the azimuthal quantum number contributes to the energy level splitting due to electron-electron interactions and shielding effects. Orbitals with different values can have different energies even if they belong to the same principal energy level.
Illustrative Explanation: Think of a crowded room where people are trying to move around. If some people are standing still (s orbitals), they take up less space, while others are moving around energetically (p, d, f orbitals). The more complex shapes of the moving people can lead to different levels of crowding and energy, illustrating how different values can affect energy levels in an atom.
3. Relationship with Other Quantum Numbers
The azimuthal quantum number is one of four quantum numbers that describe the state of an electron in an atom. The other three quantum numbers are:
A. Principal Quantum Number ()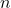
The principal quantum number indicates the main energy level of an electron and can take on positive integer values (1, 2, 3, …). The azimuthal quantum number is dependent on and can take values from to .
Illustrative Explanation: Imagine a ladder where each rung represents a principal energy level. The higher you go on the ladder (higher ), the more options you have for the shapes of the orbitals (different values) you can occupy.
B. Magnetic Quantum Number (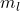
)
The magnetic quantum number describes the orientation of the orbital in space and can take on integer values ranging from 
to 
. For each value of , there are 
possible values of .
Illustrative Explanation: Picture a set of arrows representing the orientations of different orbitals. For a p orbital (), there are three orientations (one for each value: -1, 0, +1). This shows how the azimuthal quantum number determines the number of orientations available for a given shape.
C. Spin Quantum Number (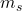
)
The spin quantum number describes the intrinsic angular momentum (spin) of an electron and can take on values of 
or 
. The spin of an electron is independent of the azimuthal quantum number but is essential for determining the overall state of the electron.
Illustrative Explanation: Imagine two dancers spinning in opposite directions. Each dancer represents an electron with a specific spin. Regardless of the shape of the dance floor (the orbital shape determined by ), the dancers can still spin in their own unique ways.
4. Applications of the Azimuthal Quantum Number
The azimuthal quantum number has several important applications in various fields:
A. Chemical Bonding and Molecular Structure
In chemistry, the azimuthal quantum number helps predict the shapes of molecules and the types of bonds that can form. Understanding the shapes of orbitals allows chemists to determine how atoms will interact and bond with one another.
Illustrative Explanation: Think of a puzzle where each piece represents an atom with specific orbital shapes. The azimuthal quantum number helps determine how these pieces fit together to form a complete picture (molecule). For example, the shapes of s and p orbitals dictate how carbon atoms bond to form complex organic molecules.
B. Spectroscopy
In spectroscopy, the azimuthal quantum number is crucial for understanding the energy levels of electrons and the transitions between them. When electrons move between different orbitals, they absorb or emit specific wavelengths of light, which can be analyzed to gain insights into the electronic structure of atoms and molecules.
Illustrative Explanation: Imagine a musical scale where each note corresponds to a specific energy level. When an electron jumps from one note (orbital) to another, it produces a sound (light) that can be measured. The azimuthal quantum number helps identify which notes (energy levels) are involved in these transitions.
C. Quantum Computing and Information Technology
In the emerging field of quantum computing, the azimuthal quantum number plays a role in understanding the behavior of qubits, the fundamental units of quantum information. The properties of electrons in different orbitals can be harnessed to create more efficient quantum systems.
Illustrative Explanation: Picture a complex circuit board where each component represents a qubit. The azimuthal quantum number helps determine how these components interact and function together, enabling the development of advanced quantum technologies.
5. Limitations and Misconceptions
While the azimuthal quantum number is a crucial concept in quantum mechanics, there are some common misconceptions and limitations:
A. Misconception: Azimuthal Quantum Number Determines Energy Alone
While the azimuthal quantum number influences the shape and angular momentum of orbitals, it does not solely determine the energy of an electron. The energy of an electron is also affected by the principal quantum number and the electron’s interactions with other electrons and the nucleus.
Illustrative Explanation: Imagine a car’s speed being influenced by both the engine’s power (principal quantum number) and the road conditions (electron interactions). The azimuthal quantum number contributes to the overall performance but is not the only factor.
B. Limitations in Multi-Electron Atoms
In multi-electron atoms, the azimuthal quantum number’s influence on energy levels can become complex due to electron-electron interactions and shielding effects. As a result, the energy levels of orbitals with the same principal quantum number may not be degenerate (equal in energy).
Illustrative Explanation: Think of a crowded elevator where people are pushing against each other. The interactions between individuals (electrons) can affect how much space each person (orbital) has, leading to variations in energy levels that are not straightforward.
6. Conclusion
In summary, the azimuthal quantum number is a fundamental concept in quantum mechanics that describes the shape of atomic orbitals and the angular momentum of electrons in an atom. By understanding the significance of the azimuthal quantum number, its relationship with other quantum numbers, and its applications in various fields, we gain valuable insights into the behavior of electrons and the structure of matter. Through illustrative examples and explanations, we can appreciate the role of the azimuthal quantum number in shaping our understanding of atomic and molecular systems. As we continue to explore the intricacies of quantum mechanics, the azimuthal quantum number will remain a cornerstone of our comprehension of the fundamental principles that govern the behavior of matter in the universe. This understanding not only enhances our knowledge of chemistry and physics but also paves the way for advancements in technology and scientific research.