In the realm of chemical kinetics, reactions are classified based on their order, which reflects the relationship between the concentration of reactants and the rate of the reaction. A second order reaction is one where the rate of reaction is directly proportional to the square of the concentration of one reactant or to the product of the concentrations of two different reactants. This classification is crucial for understanding how reactions proceed and for predicting the behavior of chemical systems under various conditions. This article aims to provide a detailed overview of second order reactions, including their characteristics, mathematical representation, mechanisms, examples, and illustrative explanations of each concept to enhance understanding.
Definition of Second Order Reactions
What is a Second Order Reaction?
A second order reaction can be defined as a reaction whose rate is proportional to the square of the concentration of one reactant or to the product of the concentrations of two reactants. Mathematically, this can be expressed in two forms:
1. Single Reactant: For a reaction of the form:
![\[ A \rightarrow \text{Products} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d1dccfed22b266d245ed3e02ed90a978_l3.png "Rendered by QuickLaTeX.com")
The rate law can be written as:
![\[ \text{Rate} = k[A]^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d9b64614568657d77f442fd788661070_l3.png "Rendered by QuickLaTeX.com")
where 
is the rate constant and ![[A]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-b2e794eaaca376db17f79ff4fb8089b8_l3.png "Rendered by QuickLaTeX.com")
is the concentration of reactant A.
2. Two Reactants: For a reaction involving two reactants:
![\[ A + B \rightarrow \text{Products} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-606179461be96c4c699e1c2c600cdcfe_l3.png "Rendered by QuickLaTeX.com")
The rate law can be expressed as:
![\[ \text{Rate} = k[A][B] \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-83f91d37e3d336aaa0be5d6ba21b67c0_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
To visualize a second order reaction, imagine a race where the speed of a car (the reaction rate) depends on the number of passengers (the concentration of reactants). If one car can carry two passengers, the speed increases significantly with each additional passenger. In this analogy, the car’s speed represents the reaction rate, and the passengers represent the concentration of the reactants. The more passengers there are, the faster the car goes, illustrating the squared relationship in a single reactant scenario or the multiplicative relationship in a two-reactant scenario.
Characteristics of Second Order Reactions
1. Rate Dependence
The rate of a second order reaction is dependent on the concentration of the reactants. For a single reactant, the rate increases with the square of its concentration, while for two reactants, the rate is proportional to the product of their concentrations. This means that if the concentration of one reactant doubles, the rate of reaction will quadruple in the case of a single reactant.
2. Units of the Rate Constant
The units of the rate constant for a second order reaction can be derived from the rate law. The rate of reaction has units of concentration per time (e.g., mol/L/s), and the concentration has units of mol/L. Therefore, for a second order reaction, the units of are:
![\[ \text{Units of } k = \frac{\text{Rate}}{[\text{A}]^2} = \frac{\text{mol/L/s}}{(\text{mol/L})^2} = \text{L/mol/s} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-68e40c3444081ea37857262b1b5b95b4_l3.png "Rendered by QuickLaTeX.com")
3. Integrated Rate Law
The integrated rate law for a second order reaction provides a relationship between the concentration of reactants and time. For a single reactant, the integrated rate law is given by:
![\[ \frac{1}{[A]} = kt + \frac{1}{[A]_0} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ca85ff22c628df46208c68784bce0427_l3.png "Rendered by QuickLaTeX.com")
Where:
- is the concentration of reactant A at time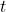
. ![[A]_0](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ab61ba0e45afdbcde627d9bec7f88817_l3.png "Rendered by QuickLaTeX.com")
is the initial concentration of reactant A.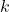- is the rate constant.
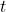- is the time elapsed.
For two reactants, the integrated rate law is more complex and depends on the initial concentrations of both reactants.
Illustrative Explanation
Imagine a garden where the growth of plants (the reaction) depends on the amount of sunlight (the concentration of a reactant). If you double the sunlight, the plants grow at a much faster rate, illustrating the squared relationship. The integrated rate law is like a growth chart that shows how the height of the plants changes over time based on the amount of sunlight they receive. The steeper the curve, the faster the growth, just as a second order reaction shows a rapid change in concentration over time.
Mechanism of Second Order Reactions
1. Elementary Reactions
Many second order reactions are elementary reactions, meaning that the reaction occurs in a single step. For example, the reaction between two molecules of nitrogen dioxide (NO₂) to form dinitrogen tetroxide (N₂O₄) can be represented as:
![\[ 2 \text{NO}_2 \rightarrow \text{N}_2\text{O}_4 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-dbac1594414a903d1d6fbd6b2ca9f453_l3.png "Rendered by QuickLaTeX.com")
The rate law for this reaction is:
![\[ \text{Rate} = k[\text{NO}_2]^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-86f5df9a320705bc8781d055077c9229_l3.png "Rendered by QuickLaTeX.com")
2. Complex Reactions
Some second order reactions may involve multiple steps or intermediates. In such cases, the overall reaction may still be second order, but the mechanism can be more complex. For example, a reaction may proceed through a series of elementary steps, each contributing to the overall rate.
Illustrative Explanation
Think of a second order reaction as a two-step dance routine. In an elementary reaction, the dancers perform their moves in perfect synchronization (a single step). In a complex reaction, the dancers may have to perform a series of intricate moves (multiple steps) before reaching the final pose (the product). Regardless of the complexity, the overall performance still reflects the second order nature of the dance.
Examples of Second Order Reactions
1. Dimerization Reactions
A classic example of a second order reaction is the dimerization of gaseous molecules. For instance, the reaction of two molecules of ethylene (C₂H₄) to form butene (C₄H₈) can be represented as:
![\[ 2 \text{C}_2\text{H}_4 \rightarrow \text{C}_4\text{H}_8 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-e35324be9357897f499916c30d89d429_l3.png "Rendered by QuickLaTeX.com")
The rate law for this reaction is:
![\[ \text{Rate} = k[\text{C}_2\text{H}_4]^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-5a3a8b61424d211cbcdee0bfc3f992af_l3.png "Rendered by QuickLaTeX.com")
2. Reactions Involving Ions
Another example is the reaction between two ions in solution, such as the reaction between hydroxide ions (OH⁻) and hydrogen ions (H⁺) to form water (H₂O):
![\[ \text{H}^+ + \text{OH}^- \rightarrow \text{H}_2\text{O} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f78791b4d2d6f1bfcfd71175ea863852_l3.png "Rendered by QuickLaTeX.com")
The rate law for this reaction is:
![\[ \text{Rate} = k[\text{H}^+][\text{OH}^-] \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-540bc4b7ecbbbc85ab36934b70269df3_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
Consider the dimerization of ethylene as a pair of dancers coming together to form a new formation. Each dancer represents a molecule of ethylene, and when they join together, they create a new structure (butene). Similarly, the reaction between hydroxide and hydrogen ions can be visualized as two friends (ions) meeting to create a new bond (water), illustrating the collaborative nature of second order reactions.
Graphical Representation
1. Concentration vs. Time
For a second order reaction, a plot of ![\frac{1}{[A]}](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-9b7aaa2e603eea6483740d251b8493b0_l3.png "Rendered by QuickLaTeX.com")
versus time () yields a straight line, indicating that the reaction follows second order kinetics. The slope of this line is equal to the rate constant .
2. Rate vs. Concentration
For a second order reaction involving two reactants, a plot of the rate versus the concentration of one reactant (while keeping the other constant) will yield a parabolic curve, reflecting the squared relationship.
Illustrative Explanation
Imagine a graph as a visual representation of a story. The straight line in the versus time plot tells a clear tale of how the concentration of reactant A decreases over time, while the parabolic curve in the rate versus concentration plot illustrates the dynamic relationship between the reactants, much like a plot twist in a story that reveals the complexity of their interaction.
Conclusion
In conclusion, second order reactions are a fundamental concept in chemical kinetics, characterized by their dependence on the concentration of reactants. Understanding their definition, characteristics, mechanisms, and examples is essential for predicting the behavior of chemical systems. Through illustrative explanations and practical examples, we can appreciate the significance of second order reactions in various fields, including organic chemistry, biochemistry, and industrial processes. As we continue to explore the intricacies of chemical kinetics, mastering the concepts surrounding second order reactions will empower chemists and researchers to design and optimize reactions for a wide range of applications, ultimately contributing to advancements in science and technology.