Newton’s Universal Law of Gravitation

Newton’s Universal Law of Gravitation is one of the cornerstones of classical physics, providing a comprehensive framework for understanding the gravitational force that governs the motion of celestial bodies and objects on Earth. Formulated by Sir Isaac Newton in the late 17th century, this law describes how every mass attracts every other mass in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This article delves into the formulation, implications, historical context, and applications of Newton’s Universal Law of Gravitation, providing a thorough understanding of this fundamental principle.

The Formulation of the Law

Newton’s Universal Law of Gravitation can be mathematically expressed as:

$F = G \frac{m_1 m_2}{r^2}$

Where:

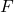$F$ is the gravitational force between two objects (measured in newtons, N).
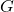$G$ is the gravitational constant, approximately $6.674 \times 10^{-11} \, \text{N m}^2/\text{kg}^2$ .
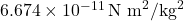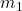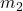$m_1$ and $m_2$ are the masses of the two objects (measured in kilograms, kg).
$r$ is the distance between the centers of the two masses (measured in meters, m).

1. Understanding the Components of the Formula

Gravitational Force ( 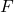$F$ ): This is the attractive force that pulls two masses toward each other. It is a vector quantity, meaning it has both magnitude and direction. The direction of the force is always toward the center of the two masses.
Gravitational Constant ( 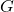$G$ ): The gravitational constant is a proportionality factor that quantifies the strength of the gravitational force in the universe. It is a very small number, indicating that gravity is a relatively weak force compared to other fundamental forces, such as electromagnetism.
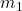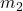Masses ( $m_1$ and $m_2$ ): The masses of the two objects involved in the gravitational interaction. The greater the mass of either object, the stronger the gravitational force between them. This is why massive bodies like planets and stars exert significant gravitational forces.
Distance ( $r$ ): The distance between the centers of the two masses. The gravitational force decreases rapidly as the distance increases, following the inverse square law. This means that if the distance between the two masses is doubled, the gravitational force becomes one-fourth as strong.

Illustrative Explanation: Imagine two basketballs (the masses) placed on a smooth surface. If you were to push them closer together, they would feel a stronger pull toward each other (gravitational force). If you were to move them apart, the pull would weaken significantly. The gravitational constant acts like a scale that tells us how strong this pull is, while the distance between the balls determines how much of that pull we actually feel.

Historical Context

The formulation of the Universal Law of Gravitation was a monumental achievement in the history of science. Before Newton, the understanding of gravity was limited, and the motion of celestial bodies was often attributed to mystical forces. Newton’s work was influenced by earlier scientists, including:

Galileo Galilei: Galileo’s experiments with falling objects laid the groundwork for understanding motion and acceleration. He demonstrated that objects fall at the same rate regardless of their mass, which was crucial for Newton’s later work.
Johannes Kepler: Kepler’s laws of planetary motion described how planets move in elliptical orbits around the Sun. Newton’s law provided the theoretical foundation for why these motions occur.
René Descartes: Descartes proposed ideas about the nature of forces and motion, which influenced Newton’s thinking.

In 1687, Newton published his seminal work, Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), where he presented his law of gravitation. This work not only revolutionized physics but also laid the foundation for classical mechanics.

Implications of the Law

Newton’s Universal Law of Gravitation has profound implications for our understanding of the universe. Some of the key implications include:

1. Motion of Celestial Bodies

The law explains the motion of planets, moons, and other celestial bodies. It accounts for the elliptical orbits of planets around the Sun, the motion of moons around planets, and the behavior of comets and asteroids.

Illustrative Explanation: Imagine the Sun as a giant magnet in the center of a playground, with planets as children on swings. The gravitational pull of the Sun keeps the planets in their orbits, just as a swing moves back and forth around a central point. The closer a child is to the center, the faster they swing, similar to how planets closer to the Sun move faster in their orbits.

2. Tides

The gravitational pull of the Moon and the Sun on Earth causes ocean tides. The varying distances between these celestial bodies and Earth result in the rise and fall of sea levels.

Illustrative Explanation: Picture a large water balloon (the Earth) with two smaller balloons (the Moon and the Sun) nearby. As the smaller balloons move around the larger one, they create bulges in the water balloon, representing high tides. When they are on opposite sides, the water level drops, creating low tides.

3. Gravitational Binding of Galaxies

The law also applies to larger scales, explaining how galaxies and galaxy clusters are held together by gravitational forces. The gravitational attraction between massive objects governs the structure and dynamics of the universe.

Illustrative Explanation: Imagine a group of friends holding hands in a circle (the galaxy). The gravitational force is like the strength of their grip, keeping them together. If one friend (a massive object) were to let go, the circle would break apart, just as galaxies can be disrupted if gravitational forces are not strong enough.

4. Escape Velocity

Newton’s law allows us to calculate the escape velocity, which is the minimum speed an object must reach to break free from a celestial body’s gravitational pull. The escape velocity from Earth is approximately 11.2 km/s.

Illustrative Explanation: Think of a rocket launching from Earth. To escape the gravitational pull, the rocket must reach a certain speed, like a ball needing to be thrown hard enough to leave a deep pit. If it doesn’t reach that speed, it will fall back down.

Applications of the Law

Newton’s Universal Law of Gravitation has numerous practical applications across various fields, including:

1. Space Exploration

Understanding gravitational forces is crucial for planning space missions. Engineers use the law to calculate trajectories, orbits, and the necessary velocities for spacecraft to reach their destinations.

Illustrative Explanation: Imagine a basketball player aiming to make a shot from a distance. They must calculate the angle and force needed to get the ball into the hoop. Similarly, mission planners calculate the trajectory of a spacecraft to ensure it reaches its target, like the Moon or Mars.

2. Satellite Technology

Satellites rely on gravitational forces to maintain their orbits around Earth. The balance between gravitational pull and the satellite’s velocity determines its orbital path.

Illustrative Explanation: Picture a child swinging a ball on a string (the satellite) around in a circle. The tension in the string (the gravitational force) keeps the ball moving in a circular path. If the child lets go, the ball will fly off in a straight line, just as a satellite would if it lost its velocity.

3. Engineering and Architecture

Gravitational forces must be considered in the design of buildings, bridges, and other structures. Engineers must ensure that structures can withstand gravitational loads and remain stable.

Illustrative Explanation: Think of a tall building as a stack of blocks. Each block (floor) must be strong enough to support the weight of the blocks above it. If the bottom block (foundation) is weak, the entire structure could collapse under the force of gravity.

4. Understanding Natural Phenomena

The law helps explain various natural phenomena, such as the motion of falling objects, the behavior of projectiles, and the dynamics of fluids under gravity.

Illustrative Explanation: Imagine dropping a feather and a rock from the same height. In a vacuum, they would hit the ground simultaneously due to gravity acting equally on both. However, in the presence of air resistance, the feather floats down slowly, while the rock falls quickly, illustrating how gravity interacts with other forces.

Limitations of Newton’s Law

While Newton’s Universal Law of Gravitation is incredibly powerful, it has limitations. It does not account for the effects of relativity, which become significant in strong gravitational fields or at very high speeds. Albert Einstein’s General Theory of Relativity provides a more comprehensive understanding of gravity, describing it as the curvature of spacetime caused by mass.

Illustrative Explanation: Imagine a trampoline (spacetime) with a heavy ball (mass) placed in the center. The ball creates a depression in the trampoline, causing smaller balls (smaller masses) placed nearby to roll toward it. This visualizes how mass influences the curvature of spacetime, leading to gravitational attraction.

Conclusion

In conclusion, Newton’s Universal Law of Gravitation is a fundamental principle that describes the gravitational force between masses and has profound implications for our understanding of the universe. Its formulation provides a mathematical framework for analyzing the motion of celestial bodies, the behavior of tides, and the dynamics of galaxies. The law has numerous practical applications in space exploration, satellite technology, engineering, and understanding natural phenomena. While it has limitations, particularly in the context of relativity, it remains a cornerstone of classical physics and continues to influence scientific thought and technological advancement. As we explore the universe and deepen our understanding of gravity, Newton’s law serves as a vital tool for unraveling the mysteries of the cosmos and the forces that govern our world. Through ongoing research and exploration, we will continue to expand our knowledge of gravitational interactions and their significance in the grand tapestry of the universe.

Blog.Pengayaan.Com