Motion in two dimensions refers to the movement of an object in a plane, characterized by changes in both the horizontal and vertical positions. This type of motion is more complex than one-dimensional motion, where an object moves along a straight line. In two-dimensional motion, we can analyze various scenarios, including projectile motion, circular motion, and general planar motion. Understanding motion in two dimensions is essential in fields such as physics, engineering, and robotics, as it provides insights into the behavior of objects in real-world situations. This article delves into the fundamental concepts, mathematical descriptions, types of motion, and applications of motion in two dimensions, providing a thorough understanding of this essential topic.
Fundamental Concepts of Motion in Two Dimensions
1. Displacement
Displacement is a vector quantity that represents the change in position of an object. It is defined as the shortest distance from the initial position to the final position, along with the direction of that distance.
- Vector Quantity: Displacement has both magnitude and direction. For example, if an object moves from point A to point B, the displacement vector points from A to B.
Illustrative Explanation: Imagine a person walking from their home (point A) to a park (point B). If they take a winding path, the distance they walked is longer than the straight line connecting their home to the park. The displacement is the straight line from home to the park, indicating both how far they are from home and in which direction.
2. Velocity
Velocity is another vector quantity that describes the rate of change of displacement with respect to time. It is defined as:
![\[ \vec{v} = \frac{\Delta \vec{d}}{\Delta t} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-7aecadaee3bd3760ff455101de9ebaa9_l3.png "Rendered by QuickLaTeX.com")
Where:
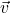is the velocity vector.
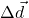is the change in displacement.
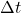is the change in time.- Average Velocity: The average velocity is calculated over a time interval and is given by the total displacement divided by the total time taken.
- Instantaneous Velocity: The instantaneous velocity is the velocity of an object at a specific moment in time.
Illustrative Explanation: Consider a car traveling from one city to another. If the car travels 100 kilometers north in 2 hours, the average velocity is 50 kilometers per hour north. If the car speeds up or slows down during the trip, the instantaneous velocity at any moment can be different from the average velocity.
3. Acceleration
Acceleration is a vector quantity that represents the rate of change of velocity with respect to time. It is defined as:
![\[ \vec{a} = \frac{\Delta \vec{v}}{\Delta t} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-599d0ceb1a05ce727f247d974e37dd48_l3.png "Rendered by QuickLaTeX.com")
Where:
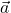is the acceleration vector.
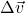is the change in velocity.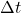- is the change in time.
- Types of Acceleration: Acceleration can be positive (speeding up), negative (slowing down, also known as deceleration), or zero (constant velocity).
Illustrative Explanation: Imagine a skateboarder pushing off the ground. As they push harder, they accelerate forward, increasing their speed. If they hit a bump and slow down, they experience negative acceleration. If they glide smoothly at a constant speed, their acceleration is zero.
Mathematical Representation of Motion in Two Dimensions
To analyze motion in two dimensions, we often use a coordinate system, typically the Cartesian coordinate system, where positions are defined by two coordinates: 
(horizontal) and 
(vertical).
1. Position Vector
The position of an object in two dimensions can be represented by a position vector 
:
![\[ \vec{r} = x \hat{i} + y \hat{j} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-ff2622f1ff964ec01e56a00271d1841a_l3.png "Rendered by QuickLaTeX.com")
Where:
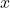- is the horizontal coordinate.
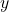- is the vertical coordinate.
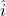and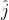 
are the unit vectors in the 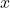and 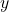directions, respectively.
Illustrative Explanation: Picture a treasure map where the treasure is located at coordinates (3, 4). The position vector points from the origin (0, 0) to the treasure, indicating how far to move right (3 units) and how far to move up (4 units).
2. Velocity Vector
The velocity vector in two dimensions can be expressed as:
![\[ \vec{v} = v_x \hat{i} + v_y \hat{j} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-80589aef4225a340467a6fe806add774_l3.png "Rendered by QuickLaTeX.com")
Where:
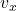is the horizontal component of velocity.
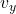is the vertical component of velocity.
Illustrative Explanation: Imagine a drone flying diagonally across a park. If it moves 5 meters per second to the right and 3 meters per second upward, its velocity vector combines these two components, showing its overall direction and speed.
3. Acceleration Vector
Similarly, the acceleration vector can be expressed as:
![\[ \vec{a} = a_x \hat{i} + a_y \hat{j} \]](https://pengayaan.com/blog/wp-content/uploads/2024/11/quicklatex.com-ea4617d86cdb1157a9fe77ca8d947e9b_l3.png "Rendered by QuickLaTeX.com")
Where:
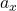is the horizontal component of acceleration.
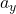is the vertical component of acceleration.
Illustrative Explanation: Consider a basketball thrown upward at an angle. As it rises, it slows down due to gravity (negative acceleration in the vertical direction) while moving horizontally. The acceleration vector combines these effects, showing how the basketball’s speed changes in both dimensions.
Types of Motion in Two Dimensions
1. Projectile Motion
Projectile motion refers to the motion of an object that is launched into the air and is subject to the force of gravity. The path followed by a projectile is a parabola, and its motion can be analyzed in two separate components: horizontal and vertical.
- Horizontal Motion: The horizontal component of motion is uniform, meaning the horizontal velocity remains constant (ignoring air resistance).
- Vertical Motion: The vertical component of motion is influenced by gravity, resulting in a downward acceleration of approximately
.
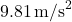Illustrative Explanation: Imagine throwing a ball from a height. As the ball travels forward, it also falls due to gravity. The combination of its horizontal motion (moving forward) and vertical motion (falling down) creates a curved path, resembling a rainbow.
2. Circular Motion
Circular motion refers to the motion of an object moving along a circular path. This type of motion can be uniform (constant speed) or non-uniform (changing speed).
- Uniform Circular Motion: In uniform circular motion, the object moves at a constant speed along a circular path. The direction of the velocity vector changes continuously, resulting in centripetal acceleration directed toward the center of the circle.
- Non-Uniform Circular Motion: In non-uniform circular motion, the object’s speed changes as it moves along the circular path, resulting in both centripetal and tangential acceleration.
Illustrative Explanation: Picture a car driving around a circular track. If the car maintains a constant speed, it experiences uniform circular motion, constantly changing direction but not speed. If the driver accelerates or decelerates while turning, the car experiences non-uniform circular motion, with changing speed and direction.
3. General Planar Motion
General planar motion encompasses any motion that occurs in a two-dimensional plane, which may not fit neatly into the categories of projectile or circular motion. This type of motion can involve complex trajectories and varying speeds.
Illustrative Explanation: Imagine a drone flying in a park, weaving in and out of trees. Its path is not a straight line or a perfect circle; instead, it follows a complex trajectory that changes direction and speed as it navigates obstacles.
Applications of Motion in Two Dimensions
Understanding motion in two dimensions has numerous practical applications across various fields:
1. Engineering and Design
Engineers use principles of two-dimensional motion to design vehicles, bridges, and buildings. They must consider forces acting on structures and how they will respond to dynamic loads.
Illustrative Explanation: Think of designing a roller coaster. Engineers must calculate the motion of the cars as they travel along the track, ensuring that the forces acting on the riders are safe and enjoyable.
2. Sports Science
In sports, analyzing the motion of athletes can improve performance and reduce injury risk. Coaches and trainers study the two-dimensional motion of players to optimize techniques and strategies.
Illustrative Explanation: Consider a soccer player kicking a ball. Coaches analyze the angle and speed of the kick to determine the best way to score a goal, taking into account the ball’s trajectory and the position of defenders.
3. Robotics and Animation
In robotics and computer animation, understanding two-dimensional motion is crucial for programming movements and creating realistic animations. Algorithms are developed to simulate motion in a plane.
Illustrative Explanation: Imagine programming a robot to navigate a maze. The robot must calculate its position and direction at each step, adjusting its path based on obstacles, similar to how a character in a video game moves through a virtual world.
4. Physics and Astronomy
In physics and astronomy, analyzing the motion of celestial bodies in two dimensions helps scientists understand orbits, gravitational interactions, and the dynamics of galaxies.
Illustrative Explanation: Picture the Earth orbiting the Sun. Scientists use two-dimensional motion principles to calculate the Earth’s path, predicting eclipses and understanding the effects of gravitational forces from other planets.
Conclusion
In conclusion, motion in two dimensions is a fundamental concept that describes the movement of objects in a plane, characterized by changes in both horizontal and vertical positions. By understanding key concepts such as displacement, velocity, and acceleration, we can analyze various types of motion, including projectile motion, circular motion, and general planar motion. The mathematical representation of motion in two dimensions provides a framework for solving problems and predicting the behavior of moving objects. The applications of this knowledge span multiple fields, including engineering, sports science, robotics, and astronomy. As we continue to explore the intricacies of motion in two dimensions, we gain valuable insights into the dynamics of the physical world, enhancing our understanding of how objects interact and move within our environment. Through ongoing research and technological advancements, our comprehension of two-dimensional motion will continue to evolve, paving the way for new discoveries and innovations that harness the principles of motion in practical and impactful ways.