The perimeter of a triangle is a fundamental concept in geometry that refers to the total distance around the triangle. Understanding how to calculate the perimeter is essential for various applications in mathematics, engineering, architecture, and everyday life. This article will provide an exhaustive exploration of the perimeter of a triangle, covering its definition, formula, properties, types of triangles, and illustrative explanations of each concept.
Definition of Perimeter
The perimeter of a triangle is defined as the sum of the lengths of all three sides of the triangle. It represents the total distance around the triangle and is typically measured in linear units such as centimeters, meters, inches, or feet.
Formula for the Perimeter of a Triangle
The formula for calculating the perimeter 
of a triangle is straightforward:
![\[ P = a + b + c \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-8a43067d4e28163f26b4f231219c8fb4_l3.png "Rendered by QuickLaTeX.com")
Where:
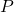- = Perimeter of the triangle
= Length of side A
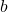= Length of side B
= Length of side C
This formula applies to all types of triangles, regardless of their shape or size.
Properties of the Perimeter of a Triangle
1. Additive Nature: The perimeter is simply the sum of the lengths of the sides. This property makes it easy to calculate as long as the lengths of all three sides are known.
2. Units of Measurement: The perimeter is expressed in the same units as the lengths of the sides. If the sides are measured in centimeters, the perimeter will also be in centimeters.
3. Non-Negative Value: The perimeter of a triangle is always a non-negative value since it is the sum of positive lengths.
4. Dependence on Side Lengths: The perimeter changes if any of the side lengths change. For example, if one side of the triangle is lengthened, the perimeter will increase accordingly.
Types of Triangles and Their Perimeters
Triangles can be classified into several types based on their side lengths and angles. The perimeter calculation remains the same, but the properties of the triangles may vary.
1. Equilateral Triangle: An equilateral triangle has all three sides of equal length. If the length of each side is 
, the perimeter can be calculated as:
![\[ P = 3s \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-9e881d1fac777125f9d9efacfced492d_l3.png "Rendered by QuickLaTeX.com")
– Illustrative Example: If each side of an equilateral triangle measures 4 cm, the perimeter would be:
![\[ P = 3 \times 4 = 12 \, \text{cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-164a8a911d324fc1cf022d5e29764077_l3.png "Rendered by QuickLaTeX.com")
2. Isosceles Triangle: An isosceles triangle has two sides of equal length. If the lengths of the equal sides are and the base is , the perimeter is:
![\[ P = 2a + b \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-923f9099169220f46ae84805ded21186_l3.png "Rendered by QuickLaTeX.com")
– Illustrative Example: For an isosceles triangle with equal sides of 5 cm and a base of 6 cm, the perimeter would be:
![\[ P = 2 \times 5 + 6 = 10 + 6 = 16 \, \text{cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-904199add94f3cd2f35487c761ff12ab_l3.png "Rendered by QuickLaTeX.com")
3. Scalene Triangle: A scalene triangle has all sides of different lengths. If the lengths of the sides are , , and , the perimeter is calculated as:
– Illustrative Example: For a scalene triangle with side lengths of 3 cm, 4 cm, and 5 cm, the perimeter would be:
![\[ P = 3 + 4 + 5 = 12 \, \text{cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-2ffa0b58e9c8ec28a2951db0bb0c74fc_l3.png "Rendered by QuickLaTeX.com")
4. Right Triangle: A right triangle has one angle that measures 90 degrees. The perimeter is still calculated using the same formula:
– Illustrative Example: For a right triangle with legs measuring 6 cm and 8 cm, and the hypotenuse calculated using the Pythagorean theorem (
), the perimeter would be:
![\[ P = 6 + 8 + 10 = 24 \, \text{cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-89bda248463530cf1f6cf12b9115bff2_l3.png "Rendered by QuickLaTeX.com")
Applications of the Perimeter of a Triangle
Understanding the perimeter of a triangle has practical applications in various fields:
1. Construction and Architecture: When designing buildings or structures, architects need to calculate the perimeter of triangular components to determine materials needed for walls, roofs, and foundations.
2. Landscaping: In landscaping, the perimeter of triangular garden beds or plots is calculated to estimate the amount of fencing or edging required.
3. Sports: In sports like track and field, the perimeter of triangular fields or areas is important for setting up events and determining distances.
4. Art and Design: Artists and designers may use the concept of perimeter when creating triangular shapes in their work, ensuring that dimensions are accurate for aesthetic purposes.
Conclusion
The perimeter of a triangle is a fundamental geometric concept that represents the total distance around the triangle. By understanding how to calculate the perimeter using the formula 
, we can apply this knowledge to various types of triangles, including equilateral, isosceles, scalene, and right triangles.
The properties of the perimeter, such as its additive nature and dependence on side lengths, make it a straightforward yet essential measurement in geometry. With applications spanning construction, landscaping, sports, and art, the perimeter of a triangle plays a vital role in both theoretical and practical contexts.
By mastering the concept of the perimeter of a triangle, we gain valuable insights into the world of geometry and its relevance in our daily lives. Whether we are designing a structure, planning a garden, or simply exploring the beauty of triangular shapes, the perimeter remains a key element in understanding and interacting with the physical world.