Trigonometric Functions: A Comprehensive Exploration

Trigonometric functions are fundamental mathematical functions that relate the angles of a triangle to the lengths of its sides. They are essential in various fields, including mathematics, physics, engineering, and computer science. Trigonometric functions are particularly useful in modeling periodic phenomena, such as sound waves, light waves, and the motion of pendulums. This article aims to provide an exhaustive overview of trigonometric functions, detailing their definitions, properties, types, and illustrative explanations for each concept.

1. Understanding Trigonometric Functions

1.1. Definition of Trigonometric Functions

Trigonometric functions are defined based on the relationships between the angles and sides of a right triangle. The primary trigonometric functions are sine (sin), cosine (cos), and tangent (tan). These functions can be defined for any angle, not just those in right triangles, by extending their definitions to the unit circle.

Illustrative Explanation: Imagine a right triangle where one angle is 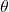$\theta$ . The side opposite this angle is called the opposite side, the side adjacent to the angle is the adjacent side, and the hypotenuse is the longest side. The trigonometric functions relate these sides to the angle $\theta$ .

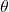1.2. The Unit Circle

The unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane. It is a powerful tool for defining trigonometric functions for all angles, including those greater than 90 degrees and negative angles. The coordinates of any point on the unit circle can be expressed as $(x, y)$ , where $x = \cos(\theta)$ and $y = \sin(\theta)$ .

Illustrative Explanation: Visualize a circle with a radius of 1. As you move around the circle, the angle 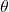$\theta$ is measured from the positive x-axis. The x-coordinate of the point on the circle gives you the cosine of the angle, while the y-coordinate gives you the sine of the angle.

2. Primary Trigonometric Functions

2.1. Sine Function

The sine function, denoted as $\sin(\theta)$ , is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle:

$\sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}$

Illustrative Explanation: If you have a right triangle where the angle 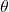$\theta$ is 30 degrees, and the hypotenuse is 10 units long, the length of the opposite side can be calculated as 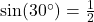$\sin(30^\circ) = \frac{1}{2}$ . Therefore, the opposite side is 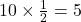$10 \times \frac{1}{2} = 5$ units.

2.2. Cosine Function

The cosine function, denoted as $\cos(\theta)$ , is defined as the ratio of the length of the adjacent side to the length of the hypotenuse:

$\cos(\theta) = \frac{\text{Adjacent}}{\text{Hypotenuse}}$

Illustrative Explanation: Continuing with the previous example, if the hypotenuse is 10 units long and the angle 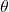$\theta$ is 30 degrees, the length of the adjacent side can be calculated as 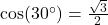$\cos(30^\circ) = \frac{\sqrt{3}}{2}$ . Therefore, the adjacent side is 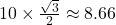$10 \times \frac{\sqrt{3}}{2} \approx 8.66$ units.

2.3. Tangent Function

The tangent function, denoted as $\tan(\theta)$ , is defined as the ratio of the sine of the angle to the cosine of the angle, or equivalently, the ratio of the opposite side to the adjacent side:

$\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} = \frac{\text{Opposite}}{\text{Adjacent}}$

Illustrative Explanation: If you have the same right triangle with an angle 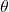$\theta$ of 30 degrees, you can find the tangent as 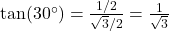$\tan(30^\circ) = \frac{1/2}{\sqrt{3}/2} = \frac{1}{\sqrt{3}}$ . This means that for every unit of length on the adjacent side, the opposite side is approximately 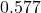$0.577$ units long.

3. Reciprocal Trigonometric Functions

In addition to the primary trigonometric functions, there are three reciprocal functions: cosecant, secant, and cotangent.

3.1. Cosecant Function

The cosecant function, denoted as $\csc(\theta)$ , is the reciprocal of the sine function:

$\csc(\theta) = \frac{1}{\sin(\theta)}$

Illustrative Explanation: If 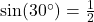$\sin(30^\circ) = \frac{1}{2}$ , then 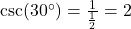$\csc(30^\circ) = \frac{1}{\frac{1}{2}} = 2$ . This means that the hypotenuse is twice the length of the opposite side.

3.2. Secant Function

The secant function, denoted as $\sec(\theta)$ , is the reciprocal of the cosine function:

$\sec(\theta) = \frac{1}{\cos(\theta)}$

Illustrative Explanation: If 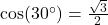$\cos(30^\circ) = \frac{\sqrt{3}}{2}$ , then 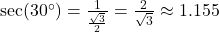$\sec(30^\circ) = \frac{1}{\frac{\sqrt{3}}{2}} = \frac{2}{\sqrt{3}} \approx 1.155$ . This indicates that the hypotenuse is approximately 1.155 times the length of the adjacent side.

3.3. Cotangent Function

The cotangent function, denoted as $\cot(\theta)$ , is the reciprocal of the tangent function:

$\cot(\theta) = \frac{1}{\tan(\theta)} = \frac{\cos(\theta)}{\sin(\theta)}$

Illustrative Explanation: If 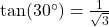$\tan(30^\circ) = \frac{1}{\sqrt{3}}$ , then 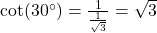$\cot(30^\circ) = \frac{1}{\frac{1}{\sqrt{3}}} = \sqrt{3}$ . This means that for every unit of length on the opposite side, the adjacent side is approximately 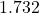$1.732$ units long.

4. Properties of Trigonometric Functions

Trigonometric functions have several important properties that are useful in various applications:

4.1. Periodicity

Trigonometric functions are periodic, meaning they repeat their values in regular intervals. The sine and cosine functions have a period of $2\pi$ radians (or 360 degrees), while the tangent function has a period of $\pi$ radians (or 180 degrees).

Illustrative Explanation: If you plot the sine function, you will see that it oscillates between -1 and 1, repeating every 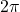$2\pi$ radians. This periodic nature is similar to the motion of a pendulum swinging back and forth.

4.2. Symmetry

Trigonometric functions exhibit specific symmetries:

Sine Function: 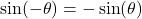$\sin(-\theta) = -\sin(\theta)$ (odd function)
Cosine Function: 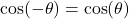$\cos(-\theta) = \cos(\theta)$ (even function)
Tangent Function: 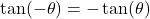$\tan(-\theta) = -\tan(\theta)$ (odd function)
Illustrative Explanation: The sine function is symmetric about the origin, meaning that if you reflect it across the origin, it looks the same. In contrast, the cosine function is symmetric about the y-axis, meaning it looks the same when reflected across the y-axis.

4.3. Pythagorean Identity

One of the most important identities in trigonometry is the Pythagorean identity, which states:

$\sin^2(\theta) + \cos^2(\theta) = 1$

This identity is derived from the Pythagorean theorem and holds true for all angles $\theta$ .

Illustrative Explanation: If you think of a right triangle inscribed in the unit circle, the lengths of the sides correspond to the sine and cosine of the angle. The Pythagorean identity shows that the square of the length of the hypotenuse (which is 1) is equal to the sum of the squares of the lengths of the other two sides.

5. Applications of Trigonometric Functions

Trigonometric functions have a wide range of applications across various fields:

5.1. Physics

In physics, trigonometric functions are used to model oscillatory motion, such as the motion of pendulums, waves, and vibrations. They help describe phenomena like sound waves and light waves.

Illustrative Explanation: When analyzing the motion of a pendulum, the height of the pendulum bob can be modeled using the sine function, showing how it oscillates back and forth over time.

5.2. Engineering

In engineering, trigonometric functions are used in fields such as civil engineering, electrical engineering, and mechanical engineering. They are essential for analyzing forces, designing structures, and understanding waveforms.

Illustrative Explanation: When designing a bridge, engineers use trigonometric functions to calculate the angles and lengths of the supporting beams, ensuring the structure can withstand various forces.

5.3. Computer Graphics

In computer graphics, trigonometric functions are used to create realistic animations and simulations. They help model rotations, oscillations, and periodic movements.

Illustrative Explanation: When animating a character walking, trigonometric functions can be used to simulate the up-and-down motion of the character’s legs, creating a lifelike walking effect.

5.4. Navigation and Surveying

Trigonometric functions are used in navigation and surveying to calculate distances and angles between points. They are essential for determining positions on maps and in the field.

Illustrative Explanation: When surveying land, surveyors use trigonometric functions to measure angles and distances, allowing them to create accurate maps and determine property boundaries.

Conclusion

In conclusion, trigonometric functions are fundamental mathematical functions that relate angles to the lengths of sides in triangles. They play a crucial role in various fields, including physics, engineering, computer graphics, and navigation. By understanding the definitions, properties, and applications of trigonometric functions, we gain valuable insights into their behavior and relevance in real-world scenarios. As we continue to study mathematics and its applications, the knowledge of trigonometric functions will remain a key component of our mathematical toolkit.

Blog.Pengayaan.Com