The concepts of critical angle and refractive index are fundamental in the study of optics, particularly in understanding how light behaves when it passes from one medium to another. This article will delve into the definitions of critical angle and refractive index, their relationship, the underlying principles, and illustrative explanations for each concept.
Definition of Refractive Index
The refractive index, denoted as 
, is a dimensionless number that describes how light propagates through a medium. It is defined as the ratio of the speed of light in a vacuum (
) to the speed of light in the medium (
). Mathematically, it is expressed as:
![\[ n = \frac{c}{v} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-8f9e2f4cb58a67965f1c352a0f7479c0_l3.png "Rendered by QuickLaTeX.com")
Where:
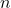- is the refractive index of the medium.
- is the speed of light in a vacuum (approximately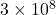
m/s). - is the speed of light in the medium.
Illustrative Explanation
To visualize the refractive index, consider a race between two runners: one running on a smooth track (light in a vacuum) and the other running on a muddy path (light in a medium). The runner on the smooth track can maintain a high speed, while the runner on the muddy path slows down significantly. The ratio of their speeds illustrates the refractive index, showing how much slower light travels in a medium compared to a vacuum.
Definition of Critical Angle
The critical angle is the angle of incidence above which total internal reflection occurs when light travels from a denser medium to a less dense medium. It is the angle at which the refracted light ray travels along the boundary between the two media, resulting in no refraction into the second medium. The critical angle (
) can be calculated using Snell’s Law, which relates the angles of incidence and refraction to the refractive indices of the two media:
![\[ n_1 \sin(\theta_1) = n_2 \sin(\theta_2) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-8b344e79e85a28a48d549870b3c7faf9_l3.png "Rendered by QuickLaTeX.com")
When light travels from a medium with a higher refractive index (
) to a medium with a lower refractive index (
), the critical angle can be defined as:
![\[ \theta_c = \arcsin\left(\frac{n_2}{n_1}\right) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-20036ec9f9d9fffcf8887f3d76bb240e_l3.png "Rendered by QuickLaTeX.com")
Where:
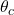- is the critical angle.
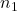- is the refractive index of the denser medium.
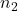- is the refractive index of the less dense medium.
Illustrative Explanation
To illustrate the critical angle, imagine a water slide that leads into a swimming pool. As you approach the edge of the slide (the boundary between water and air), there is a specific angle at which you can slide off into the pool. If you go beyond that angle, you will not enter the pool but instead bounce back into the slide. This angle represents the critical angle, where the transition from sliding into the pool (refraction) to bouncing back (total internal reflection) occurs.
Relationship Between Critical Angle and Refractive Index
The relationship between the critical angle and the refractive index is direct and can be understood through the formula for the critical angle derived from Snell’s Law. As mentioned earlier, the critical angle is given by:
From this equation, we can observe the following key points regarding the relationship between critical angle and refractive index:
1. Higher Refractive Index of the Denser Medium: As the refractive index of the denser medium () increases, the critical angle () decreases. This means that light must strike the boundary at a smaller angle to achieve total internal reflection.
Illustrative Explanation
Imagine a thick glass block (high refractive index) placed in water (lower refractive index). If you shine a light beam at the glass-water boundary, the critical angle will be smaller compared to shining the same beam at a boundary between air and water. The thicker the glass (higher ), the less steep the angle needs to be for total internal reflection to occur.
2. Lower Refractive Index of the Less Dense Medium: As the refractive index of the less dense medium () decreases, the critical angle () increases. This means that light can strike the boundary at a larger angle before total internal reflection occurs.
Illustrative Explanation
Consider a scenario where light travels from glass (higher refractive index) to air (lower refractive index). If the air’s refractive index decreases (for example, due to changes in temperature or pressure), the critical angle will increase, allowing light to strike the boundary at a larger angle before being totally internally reflected.
3. Total Internal Reflection: Total internal reflection occurs only when light travels from a medium with a higher refractive index to one with a lower refractive index. If the angle of incidence exceeds the critical angle, all the light is reflected back into the denser medium.
Illustrative Explanation
Think of a flashlight beam directed at the surface of a pond. If you shine the flashlight at a shallow angle, the light will enter the water (refraction). However, if you increase the angle beyond a certain point (the critical angle), the light will reflect off the surface of the water and not enter it at all. This phenomenon is total internal reflection, which is crucial in applications like fiber optics.
Applications of Critical Angle and Refractive Index
Understanding the relationship between critical angle and refractive index has several practical applications:
1. Fiber Optics: Fiber optic cables utilize total internal reflection to transmit light signals over long distances. The design of these cables ensures that light remains within the core by maintaining angles greater than the critical angle.
Illustrative Explanation
Imagine a long, flexible tube filled with water. If you shine a light into one end at the right angle, it travels through the tube without escaping. This is similar to how light travels through fiber optic cables, reflecting off the walls and maintaining its path.
2. Optical Instruments: Lenses and prisms in optical devices, such as cameras and microscopes, rely on the principles of refraction and critical angles to focus light and create clear images.
Illustrative Explanation
Consider a camera lens that captures light from a scene. The lens is designed to bend (refract) the light at specific angles, ensuring that the image is focused correctly on the sensor. The critical angle plays a role in how light interacts with the lens materials.
3. Total Internal Reflection in Nature: Natural phenomena, such as the shimmering effect seen on the surface of a lake or the sparkle of a diamond, are due to total internal reflection. Understanding the critical angle helps explain these visual effects.
Illustrative Explanation
Picture a diamond ring sparkling in the sunlight. The light entering the diamond reflects off its facets at angles greater than the critical angle, creating a brilliant display of colors. This effect is a direct result of the relationship between critical angle and refractive index.
Conclusion
In conclusion, the relationship between critical angle and refractive index is a fundamental concept in optics that helps us understand how light behaves when transitioning between different media. The critical angle is determined by the refractive indices of the two media, influencing whether light will be refracted or totally internally reflected. By grasping these concepts and their applications, we can better appreciate the intricate behavior of light in various contexts, from everyday experiences to advanced technological applications. Understanding this relationship not only enhances our knowledge of optics but also informs the design and functionality of numerous optical devices and systems.