In the study of wave phenomena, particularly in physics and engineering, the concepts of phase velocity and group velocity are fundamental to understanding how waves propagate through different media. These two velocities describe different aspects of wave motion and are crucial in various applications, including optics, acoustics, and quantum mechanics. This article will provide a detailed exploration of the relationship between group velocity and phase velocity, including definitions, mathematical formulations, illustrative explanations, and applications.
1. Definitions of Phase Velocity and Group Velocity
A. Phase Velocity
Phase velocity is defined as the speed at which a particular phase of the wave (such as a crest or trough) propagates through space. It is given by the formula:
![\[ v_p = \frac{\omega}{k} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-afddb4f6836237a00a58a5a919150141_l3.png "Rendered by QuickLaTeX.com")
Where:
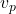is the phase velocity,
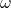is the angular frequency of the wave (in radians per second),
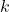is the wave number (in radians per meter), which is related to the wavelength 
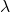by the equation 
.
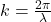Illustrative Explanation: Imagine a series of ocean waves approaching the shore. The phase velocity is like the speed at which a specific crest of a wave travels towards the beach. If you were to stand on the shore and watch a particular crest, you would measure how fast it moves across the water.
B. Group Velocity
Group velocity, on the other hand, is defined as the speed at which the overall shape of the wave’s amplitudes (the envelope of the wave) propagates through space. It is given by the formula:
![\[ v_g = \frac{d\omega}{dk} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-2be56d2b8bc57f67c22c9376ceae6d0a_l3.png "Rendered by QuickLaTeX.com")
Where:
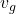is the group velocity,
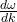represents the derivative of angular frequency with respect to wave number.
Illustrative Explanation: Continuing with the ocean wave analogy, the group velocity is like the speed at which a group of waves (or a wave packet) moves towards the shore. If you were to observe a series of crests and troughs that form a larger wave packet, the group velocity would be the speed at which that entire packet travels.
2. Mathematical Relationship Between Group Velocity and Phase Velocity
The relationship between group velocity and phase velocity can be understood through the dispersion relation, which describes how the phase velocity varies with frequency. In many cases, the two velocities are related by the following equation:
![\[ v_g = v_p - \lambda \frac{dv_p}{d\lambda} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-401674637235051886950e97a7d6047b_l3.png "Rendered by QuickLaTeX.com")
Where:
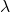- is the wavelength,
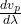is the rate of change of phase velocity with respect to wavelength.
This equation indicates that the group velocity can be influenced by how the phase velocity changes with wavelength. In non-dispersive media, where the phase velocity is constant regardless of wavelength, the group velocity equals the phase velocity:
![\[ v_g = v_p \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-e7354369c592c04f19bea24598c69668_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation: Imagine a train moving along a track. If the train (representing the wave packet) moves at a constant speed (non-dispersive medium), the speed of the individual cars (representing the phase velocity) is the same as the speed of the entire train. However, if the track has varying slopes (dispersive medium), the speed of the train may differ from the speed of the individual cars, illustrating how group velocity can differ from phase velocity.
3. Physical Interpretation of Group and Phase Velocity
A. Wave Propagation in Different Media
In dispersive media, different frequencies travel at different speeds, leading to a separation of wave packets over time. This phenomenon is crucial in understanding how signals propagate in optical fibers, where different wavelengths of light can travel at different speeds, affecting the overall signal integrity.
Illustrative Explanation: Consider a marching band playing different musical notes. If each section of the band (representing different frequencies) moves at a different speed, the overall sound (the wave packet) may become distorted as the sections spread apart. This illustrates how group velocity can differ from phase velocity in dispersive media.
B. Applications in Communication and Signal Processing
In telecommunications, understanding the relationship between group velocity and phase velocity is essential for designing efficient transmission systems. For example, in fiber optics, the group velocity determines how quickly information can be transmitted, while the phase velocity affects the characteristics of the light wave.
Illustrative Explanation: Imagine sending a message through a series of tubes filled with different gases. The speed at which the message (the wave packet) travels through the tubes (group velocity) will depend on the properties of the gas (the medium), while the speed of individual air molecules (phase velocity) may vary. Understanding both velocities helps ensure that the message arrives quickly and clearly.
4. Examples of Group and Phase Velocity
A. Electromagnetic Waves
In free space, electromagnetic waves (such as light) travel at the speed of light 
. In this case, both the phase velocity and group velocity are equal:
![\[ v_p = v_g = c \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-62b7e25666a3849e1e676d16b4407acd_l3.png "Rendered by QuickLaTeX.com")
However, in a medium like glass, the phase velocity is reduced due to the medium’s refractive index 
:
![\[ v_p = \frac{c}{n} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-3200c363c834bef5bfd94606c9fae4c3_l3.png "Rendered by QuickLaTeX.com")
The group velocity can be calculated using the dispersion relation, which may lead to 
.
Illustrative Explanation: Think of light traveling through air versus glass. In air, light travels quickly (both phase and group velocity are equal), but when it enters glass, it slows down (phase velocity decreases), and the group velocity may also change, affecting how quickly information can be transmitted through the medium.
B. Sound Waves
In acoustics, sound waves traveling through air exhibit different speeds depending on frequency due to dispersion. For example, lower frequencies may travel faster than higher frequencies, leading to a difference between group and phase velocities.
Illustrative Explanation: Imagine a concert where the bass notes (low frequencies) reach the audience before the higher notes. The group velocity of the overall sound (the music) may differ from the phase velocity of individual frequencies, illustrating how sound waves can behave in a dispersive medium.
5. Conclusion
In summary, the relationship between group velocity and phase velocity is a fundamental concept in wave theory that has significant implications in various fields, including physics, engineering, and telecommunications. While phase velocity describes the speed of individual wave phases, group velocity represents the speed of the overall wave packet. Understanding this relationship is crucial for analyzing wave propagation in different media, designing communication systems, and interpreting various physical phenomena. By grasping the concepts of phase and group velocity, we can better appreciate the complexities of wave behavior and its applications in the real world.