The Volume of a Cylinder: A Comprehensive Exploration

The volume of a cylinder is a fundamental concept in geometry and mathematics that has significant applications in various fields, including engineering, architecture, manufacturing, and everyday life. Understanding how to calculate the volume of a cylinder is essential for solving problems related to capacity, material requirements, and spatial analysis. This article aims to provide an exhaustive overview of the volume of a cylinder, including its definition, formula, derivation, properties, applications, and illustrative explanations for each concept.

1. Definition of a Cylinder

1.1. What is a Cylinder?

A cylinder is a three-dimensional geometric shape with two parallel circular bases connected by a curved surface at a fixed distance from the center of the circles. The distance between the bases is known as the height of the cylinder.

Illustrative Explanation: Imagine a soup can. The can has two circular ends (the top and bottom) and a curved surface that wraps around the sides. This shape is a perfect example of a cylinder.

1.2. Notation and Terminology

Radius (r): The distance from the center of the circular base to any point on its circumference.
Height (h): The perpendicular distance between the two circular bases.
Base: The circular ends of the cylinder.

2. Formula for the Volume of a Cylinder

2.1. Volume Formula

The volume $V$ of a cylinder can be calculated using the formula:

$V = \pi r^2 h$

where $V$ is the volume, $r$ is the radius of the base, and $h$ is the height of the cylinder.

Illustrative Explanation: If you have a cylinder with a radius of $3$ units and a height of $5$ units, you can calculate its volume as follows:

$V = \pi (3^2)(5) = \pi (9)(5) = 45\pi \text{ cubic units} \approx 141.37 \text{ cubic units}$

2.2. Understanding the Components of the Formula

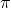$\pi$ : This constant (approximately 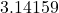$3.14159$ ) represents the ratio of the circumference of a circle to its diameter. It is crucial in calculations involving circular shapes.
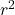$r^2$ : The radius is squared in the formula, indicating that the area of the base (which is a circle) is proportional to the square of the radius.
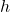$h$ : The height of the cylinder represents how tall the cylinder is, and it directly affects the volume. A taller cylinder will have a greater volume.

3. Derivation of the Volume Formula

3.1. Understanding the Base Area

The volume of a cylinder can be derived by first calculating the area of the circular base. The area $A$ of a circle is given by:

$A = \pi r^2$

3.2. Extending the Base Area to Height

To find the volume of the cylinder, we can think of the cylinder as a stack of many infinitesimally thin circular disks (or slices) stacked on top of each other from the bottom base to the top base. The volume of each disk can be approximated as the area of the base multiplied by an infinitesimally small height $dh$ .

Illustrative Explanation: Imagine slicing the cylinder into very thin disks. Each disk has a volume equal to the area of the base times its thickness. If you sum the volumes of all these disks from the bottom to the top, you get the total volume of the cylinder.

3.3. Integrating the Volume

By integrating the area of the base over the height of the cylinder, we arrive at the formula for the volume:

$V = A \cdot h = \pi r^2 \cdot h$

4. Properties of the Volume of a Cylinder

4.1. Dependence on Radius and Height

The volume of a cylinder is directly proportional to both the square of the radius and the height. This means that if either the radius or the height increases, the volume will increase significantly.

Illustrative Explanation: If the radius of a cylinder doubles while keeping the height constant, the volume increases by a factor of four (since $2^2 = 4$ ). Similarly, if the height doubles, the volume also doubles.

4.2. Units of Measurement

The volume of a cylinder is expressed in cubic units. If the radius and height are measured in meters, the volume will be in cubic meters ( $m^3$ ).

4.3. Symmetry

A cylinder is symmetrical around its central axis, meaning that its volume remains the same regardless of how it is oriented. This property is crucial in applications where uniformity is required.

5. Applications of the Volume of a Cylinder

5.1. Engineering and Manufacturing

In engineering and manufacturing, the volume of cylinders is essential for designing pipes, tanks, and other cylindrical structures. Understanding the volume helps in determining material requirements and structural integrity.

Illustrative Explanation: When designing a water tank, engineers must calculate the volume to ensure it can hold the desired amount of water.

5.2. Fluid Dynamics

In fluid dynamics, the volume of a cylinder is used to calculate the flow rates of liquids through pipes and tubes. Understanding the volume helps engineers design systems for efficient fluid transport.

Illustrative Explanation: The volume of a cylindrical pipe can be used to determine how much water can flow through it in a given time, which is crucial for plumbing and irrigation systems.

5.3. Food and Beverage Industry

In the food and beverage industry, the volume of cylindrical containers (such as cans and bottles) is important for packaging and distribution. Understanding the volume helps manufacturers determine how much product can be stored or transported.

Illustrative Explanation: A soda can is a cylinder, and its volume determines how much soda it can hold, which is essential for labeling and marketing.

5.4. Architecture

In architecture, the volume of cylindrical structures, such as columns and silos, is important for understanding their capacity and structural properties. Architects must consider the volume when designing buildings and other structures.

Illustrative Explanation: A cylindrical column in a building must be designed to support a certain volume of weight, which is crucial for the safety and stability of the structure.

6. Limitations of the Volume Formula

6.1. Assumption of Perfect Cylinders

The formula for the volume of a cylinder assumes that the object is a perfect cylinder. In reality, many objects are not perfectly cylindrical, which can lead to inaccuracies in calculations.

6.2. Complex Shapes

For complex shapes that approximate a cylinder, such as frustums (truncated cylinders) or irregular objects, the volume may require more advanced mathematical techniques to calculate accurately.

6.3. Measurement Errors

In practical applications, measurement errors in determining the radius or height can lead to significant discrepancies in the calculated volume. Precision in measurement is crucial for accurate results.

Conclusion

In conclusion, the volume of a cylinder is a fundamental concept in geometry characterized by the formula $V = \pi r^2 h$ . Understanding its definition, derivation, properties, and applications is essential for students and professionals in various fields. The volume of a cylinder plays a vital role in engineering, manufacturing, fluid dynamics, food and beverage packaging, and architecture, providing insights into the behavior and characteristics of cylindrical objects. By mastering the concept of the volume of a cylinder, individuals can enhance their problem-solving skills and deepen their understanding of geometric relationships. As we continue to explore the world of geometry, the study of the volume of a cylinder will remain an essential part of our understanding of three-dimensional shapes and their properties, paving the way for more advanced mathematical concepts and applications.

Blog.Pengayaan.Com