Single Slit Diffraction: Principles, Mechanisms, and Applications

Single slit diffraction is a fundamental phenomenon in wave optics that occurs when a wavefront encounters a narrow aperture or slit. This effect is a direct consequence of the wave nature of light and illustrates how light behaves when it passes through an opening. The resulting pattern of light and dark bands, known as a diffraction pattern, provides valuable insights into the properties of waves and the principles of interference. This article aims to provide an exhaustive overview of single slit diffraction, detailing its definition, underlying principles, mathematical formulation, experimental observations, and illustrative explanations of each concept.

Understanding Single Slit Diffraction

1. Definition of Single Slit Diffraction

Single slit diffraction refers to the bending and spreading of waves, particularly light waves, as they pass through a narrow slit. When coherent light (light waves that are in phase) strikes a single slit, it produces a characteristic pattern of alternating bright and dark fringes on a screen placed behind the slit. This phenomenon is a direct result of the interference of light waves emanating from different points within the slit.

Illustrative Explanation: Imagine a calm pond where you drop a pebble. The ripples created by the pebble represent waves. As the ripples reach the edge of a narrow dock (the slit), they bend and spread out, creating a pattern of waves on the other side. Similarly, when light passes through a single slit, it spreads out and forms a diffraction pattern.

2. Principles of Single Slit Diffraction

Single slit diffraction is governed by several key principles that explain how and why this phenomenon occurs:

a. Wave Nature of Light

The wave nature of light is a fundamental concept in optics. Light behaves as a wave, exhibiting properties such as interference and diffraction. When light waves encounter an obstacle or aperture, they can bend around it and spread out, leading to diffraction patterns.

Illustrative Explanation: Think of a group of people walking in a straight line toward a narrow doorway. As they pass through the doorway, they spread out into the room. This spreading is analogous to how light waves behave when they pass through a slit.

b. Huygens’ Principle

Huygens’ principle states that every point on a wavefront can be considered a source of secondary wavelets that spread out in all directions. The new wavefront is formed by the superposition of these wavelets. In the context of single slit diffraction, each point within the slit acts as a source of wavelets, contributing to the overall diffraction pattern.

Illustrative Explanation: Imagine a group of musicians playing different instruments in a band. Each musician (point on the wavefront) contributes to the overall sound (new wavefront) that the audience hears. Similarly, each point in the slit contributes to the diffraction pattern observed on the screen.

c. Interference of Waves

Interference occurs when two or more waves overlap and combine to form a new wave pattern. In single slit diffraction, the wavelets emerging from different points within the slit interfere with one another, leading to constructive and destructive interference. Constructive interference results in bright fringes, while destructive interference leads to dark fringes.

Illustrative Explanation: Picture two people singing in harmony. When their voices (waves) align perfectly, the sound is louder (constructive interference). However, if they sing out of sync, the sound may cancel out (destructive interference). This concept applies to the light waves passing through the slit.

3. Mathematical Formulation of Single Slit Diffraction

The diffraction pattern produced by a single slit can be quantitatively described using mathematical equations. The key parameters involved in the analysis of single slit diffraction include the slit width ( $a$ ), the wavelength of light ( $\lambda$ ), and the distance from the slit to the screen ( $L$ ).

a. Condition for Minima

The positions of the dark fringes (minima) in the diffraction pattern can be determined using the following equation:

$a \sin(\theta) = m\lambda$

Where:

$a$ is the width of the slit,
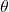$\theta$ is the angle of diffraction,
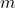$m$ is the order of the minimum (where $m = 1, 2, 3, \ldots$ ),
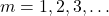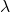$\lambda$ is the wavelength of the light.

This equation indicates that dark fringes occur at specific angles where the path difference between the wavelets from the slit leads to destructive interference.

Illustrative Explanation: Imagine a group of friends throwing balls at a target. If they throw the balls at specific angles (like the minima), some balls will miss the target entirely (dark fringes), while others will hit the target (bright fringes).

b. Intensity Distribution

The intensity of the light at any point on the screen can be described by the following equation:

$I(\theta) = I_0 \left( \frac{\sin(\beta)}{\beta} \right)^2$

Where:

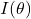$I(\theta)$ is the intensity at angle $\theta$ ,
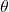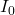$I_0$ is the maximum intensity,
$\beta = \frac{a \sin(\theta)}{\lambda}$ .

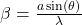This equation shows how the intensity of light varies across the diffraction pattern, with the central maximum being the brightest and the intensity decreasing for subsequent maxima and minima.

Illustrative Explanation: Think of a flashlight beam shining through a foggy night. The brightest spot (central maximum) is where the light is most concentrated, while the surrounding areas (minima) are dimmer, illustrating how intensity varies in the diffraction pattern.

4. Experimental Observations of Single Slit Diffraction

Single slit diffraction can be observed experimentally using a simple setup involving a coherent light source, a single slit, and a screen. The following steps outline a typical experimental procedure:

a. Setup

1. Coherent Light Source: Use a laser or monochromatic light source to ensure that the light waves are in phase.
2. Single Slit: Place a narrow slit (typically a few micrometers wide) in front of the light source.
3. Screen: Position a screen at a distance $L$ from the slit to observe the diffraction pattern.

b. Observation

When the coherent light passes through the slit, it produces a pattern of alternating bright and dark fringes on the screen. The central maximum is the brightest and widest fringe, with subsequent minima and maxima appearing on either side.

Illustrative Explanation: Imagine a painter using a brush to create a gradient on a canvas. The central area (central maximum) is the most vibrant, while the edges (minima) fade into the background. This visualizes how the intensity of light varies in the diffraction pattern.

5. Applications of Single Slit Diffraction

Single slit diffraction has several important applications across various fields, including:

a. Optical Instruments

Single slit diffraction principles are fundamental in the design of optical instruments, such as telescopes and microscopes. Understanding diffraction patterns helps improve the resolution and clarity of images produced by these devices.

Illustrative Explanation: Think of a camera lens that captures images. Just as the lens focuses light to create a clear picture, understanding diffraction helps optimize the performance of optical instruments.

b. Spectroscopy

In spectroscopy, single slit diffraction is used to analyze the spectral composition of light. By studying the diffraction patterns produced by different wavelengths, scientists can identify the chemical composition of substances.

Illustrative Explanation: Imagine a prism separating white light into a rainbow of colors. Similarly, single slit diffraction allows scientists to analyze light and determine the materials present based on their unique spectral signatures.

c. Communication Technologies

Single slit diffraction principles are applied in communication technologies, such as fiber optics. Understanding how light behaves when passing through narrow channels helps improve data transmission efficiency.

Illustrative Explanation: Picture a highway with multiple lanes. Just as cars (data) travel efficiently on a well-designed highway, understanding diffraction helps optimize the flow of light in communication systems.

d. Quantum Mechanics

Single slit diffraction experiments have implications in quantum mechanics, particularly in demonstrating wave-particle duality. The behavior of particles, such as electrons, in diffraction experiments provides insights into the fundamental nature of matter.

Illustrative Explanation: Imagine a magician performing a trick where a rabbit appears and disappears. The rabbit’s behavior (particles) can be surprising, just as the behavior of particles in diffraction experiments challenges our classical intuitions.

Conclusion

In conclusion, single slit diffraction is a fundamental phenomenon in wave optics that illustrates the wave nature of light and the principles of interference. By exploring its definition, underlying principles, mathematical formulation, experimental observations, and applications, we can appreciate the significance of single slit diffraction in understanding the behavior of light and waves. The study of single slit diffraction not only deepens our understanding of optics but also highlights the importance of these principles in various scientific and technological fields. As research in wave optics continues to evolve, the applications of single slit diffraction will undoubtedly expand, paving the way for innovations that can benefit society as a whole. Understanding single slit diffraction is essential for anyone interested in physics, engineering, and optics, providing a foundation for further exploration of the fascinating world of wave phenomena.

Blog.Pengayaan.Com