Stefan-Boltzmann Constant: A Comprehensive Exploration of Its Definition, Significance, and Applications

The Stefan-Boltzmann constant is a fundamental physical constant that plays a crucial role in the field of thermodynamics and astrophysics. It relates to the amount of thermal radiation emitted by a black body in terms of its temperature. Understanding the Stefan-Boltzmann constant is essential for studying heat transfer, radiation, and the behavior of stars and other celestial bodies. This article aims to provide an exhaustive overview of the Stefan-Boltzmann constant, detailing its definition, derivation, significance, applications, and illustrative explanations of each concept.

Understanding the Stefan-Boltzmann Constant

1. Definition of the Stefan-Boltzmann Constant

The Stefan-Boltzmann constant, denoted by the symbol $\sigma$ , is defined as the proportionality constant in the Stefan-Boltzmann law, which states that the total energy radiated per unit surface area of a black body is directly proportional to the fourth power of its absolute temperature. The mathematical expression of this law is given by:

$E = \sigma T^4$

Where:

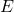$E$ is the total energy radiated per unit area (in watts per square meter, W/m²),
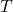$T$ is the absolute temperature of the black body (in kelvins, K),
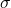$\sigma$ is the Stefan-Boltzmann constant, approximately equal to $5.67 \times 10^{-8} \, \text{W/m}^2\text{K}^4$ .
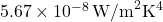Illustrative Explanation: Imagine a glowing hot metal object, like a piece of iron heated in a forge. As the temperature of the iron increases, it emits more thermal radiation, which we can see as a bright orange or yellow color. The Stefan-Boltzmann constant quantifies this relationship, indicating that as the temperature rises, the energy emitted increases dramatically.

2. Derivation of the Stefan-Boltzmann Constant

The Stefan-Boltzmann law is derived from the principles of thermodynamics and the laws of black body radiation. The derivation involves several key concepts:

a. Black Body Radiation

A black body is an idealized physical object that absorbs all incident electromagnetic radiation, regardless of frequency or angle. It is also a perfect emitter of radiation. The spectral distribution of radiation emitted by a black body is described by Planck’s law.

Illustrative Explanation: Think of a black body as a perfect sponge for light. Just as a sponge absorbs all water that touches it, a black body absorbs all radiation that falls on it. When it heats up, it emits radiation across a wide range of wavelengths.

b. Planck’s Law

Planck’s law describes the intensity of radiation emitted by a black body as a function of wavelength and temperature. It shows that the energy emitted at different wavelengths varies with temperature.

Illustrative Explanation: Imagine a rainbow created by sunlight passing through a prism. Each color represents a different wavelength of light. Planck’s law tells us how much energy is emitted at each color (wavelength) for a given temperature.

c. Integration of Planck’s Law

To derive the Stefan-Boltzmann law, one integrates Planck’s law over all wavelengths. This integration leads to the conclusion that the total energy emitted per unit area is proportional to the fourth power of the absolute temperature.

Illustrative Explanation: Picture filling a container with different colored balls, where each color represents a different wavelength of light. If you want to find the total number of balls (energy) in the container, you would need to count all the balls of every color. Similarly, integrating Planck’s law allows us to calculate the total energy emitted across all wavelengths.

3. Significance of the Stefan-Boltzmann Constant

The Stefan-Boltzmann constant is significant for several reasons:

a. Understanding Thermal Radiation

The constant provides a quantitative measure of how much energy is radiated by an object based on its temperature. This understanding is crucial in fields such as thermodynamics, astrophysics, and climate science.

Illustrative Explanation: Consider a light bulb. The hotter the filament inside the bulb, the more light and heat it emits. The Stefan-Boltzmann constant helps us calculate how much energy the bulb radiates based on its temperature.

b. Astrophysics and Cosmology

In astrophysics, the Stefan-Boltzmann constant is used to estimate the luminosity (total energy output) of stars and other celestial bodies. By measuring the temperature of a star, astronomers can determine how much energy it emits.

Illustrative Explanation: Imagine observing a distant star through a telescope. By measuring its color (which indicates temperature), astronomers can use the Stefan-Boltzmann constant to calculate how much energy the star radiates into space.

c. Climate Science

The Stefan-Boltzmann constant is also important in climate science, where it helps model the Earth’s energy balance. It is used to understand how much energy the Earth receives from the Sun and how much it radiates back into space.

Illustrative Explanation: Think of the Earth as a giant radiator. The Sun heats the Earth, and the Stefan-Boltzmann constant helps scientists calculate how much heat the Earth radiates back into the atmosphere and space, influencing climate patterns.

4. Applications of the Stefan-Boltzmann Constant

The Stefan-Boltzmann constant has numerous applications across various fields, including:

a. Engineering and Design

In engineering, the Stefan-Boltzmann constant is used in the design of thermal systems, such as radiators, heat exchangers, and insulation materials. Understanding how materials emit and absorb thermal radiation is essential for optimizing energy efficiency.

Illustrative Explanation: When designing a radiator for a heating system, engineers must consider how much heat the radiator will emit based on its temperature. The Stefan-Boltzmann constant helps them calculate the optimal size and material for efficient heating.

b. Astronomy

Astronomers use the Stefan-Boltzmann constant to estimate the sizes and temperatures of stars. By measuring the brightness of a star and applying the constant, they can infer its temperature and luminosity.

Illustrative Explanation: Imagine measuring the brightness of a star with a photometer. By applying the Stefan-Boltzmann law, astronomers can determine how hot the star is and how much energy it emits, providing insights into its life cycle and evolution.

c. Thermal Imaging

In thermal imaging technology, the Stefan-Boltzmann constant is used to analyze the thermal radiation emitted by objects. This technology is widely used in various applications, including building inspections, medical diagnostics, and surveillance.

Illustrative Explanation: Consider a thermal camera used to detect heat leaks in a building. The camera measures the thermal radiation emitted by walls and windows, and the Stefan-Boltzmann constant helps interpret the data to identify areas that need insulation.

d. Climate Modeling

In climate modeling, the Stefan-Boltzmann constant is used to understand the Earth’s energy balance and the effects of greenhouse gases. It helps scientists predict how changes in temperature will affect the Earth’s climate.

Illustrative Explanation: Think of the Earth as a giant greenhouse. The Stefan-Boltzmann constant helps scientists model how much energy is trapped by greenhouse gases and how it affects global temperatures, allowing for better climate predictions.

Conclusion

In conclusion, the Stefan-Boltzmann constant is a fundamental physical constant that quantifies the relationship between temperature and thermal radiation emitted by a black body. By exploring its definition, derivation, significance, applications, and illustrative explanations, we can appreciate the importance of the Stefan-Boltzmann constant in various fields, including thermodynamics, astrophysics, engineering, and climate science. Understanding this constant not only enhances our knowledge of thermal radiation but also provides valuable insights into the behavior of stars, the design of thermal systems, and the dynamics of Earth’s climate. As research in physics and related fields continues to evolve, the Stefan-Boltzmann constant will remain a critical tool for analyzing and understanding the complex interactions between temperature, energy, and radiation in our universe.

Blog.Pengayaan.Com