Surface area and volume are fundamental concepts in geometry that describe the size and space occupied by three-dimensional objects. Understanding these concepts is essential for various applications in mathematics, science, engineering, and everyday life. This article will delve into the definitions of surface area and volume, the formulas for calculating them for different geometric shapes, and illustrative explanations for each concept.
Definitions
Surface Area
Surface area is the total area that the surface of a three-dimensional object occupies. It is measured in square units (e.g., square meters, square centimeters). The surface area provides insight into the extent of the outer layer of an object and is crucial in applications such as material estimation, painting, and packaging.
Volume
Volume is the amount of space that a three-dimensional object occupies. It is measured in cubic units (e.g., cubic meters, cubic centimeters). Volume is essential for understanding capacity, such as how much liquid a container can hold or the amount of space available within an object.
Surface Area and Volume Formulas for Common Geometric Shapes
1. Cube
- Surface Area: The surface area
of a cube with side length 
is calculated using the formula:
![\[ A = 6s^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-056323d7cc2a06b6c18df5bcf1c2a699_l3.png "Rendered by QuickLaTeX.com")
This formula arises because a cube has six identical square faces.
- Volume: The volume
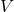of a cube is given by:
![\[ V = s^3 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-b7fbe960f22a289de7b5a5d5a5d2ec24_l3.png "Rendered by QuickLaTeX.com")
This formula indicates that the volume is the cube of the side length.
Illustrative Explanation
Imagine a cube with a side length of 2 cm. To find the surface area:
![\[ A = 6(2^2) = 6 \times 4 = 24 \text{ cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-fd7ef5a295ce9ed3fe75e82e89a0fa99_l3.png "Rendered by QuickLaTeX.com")
To find the volume:
![\[ V = 2^3 = 8 \text{ cm}^3 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-0c7b4347b684d026064db08027f9587c_l3.png "Rendered by QuickLaTeX.com")
This means the cube has a surface area of 24 square centimeters and a volume of 8 cubic centimeters.
2. Rectangular Prism
- Surface Area: The surface area of a rectangular prism with length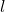
, width 
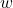, and height 
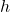is calculated as:
![\[ A = 2(lw + lh + wh) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ef5337e1fcd2a20636fcf4bbcfaeeced_l3.png "Rendered by QuickLaTeX.com")
- Volume: The volume 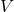of a rectangular prism is given by:
![\[ V = l \times w \times h \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ae472b769334198635dceb95e1ce6bbc_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
Consider a rectangular prism with dimensions 
cm, 
cm, and 
cm. To find the surface area:
![\[ A = 2(3 \times 4 + 3 \times 5 + 4 \times 5) = 2(12 + 15 + 20) = 2 \times 47 = 94 \text{ cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-35b97f34b1fd723af395a9d83bf4391d_l3.png "Rendered by QuickLaTeX.com")
To find the volume:
![\[ V = 3 \times 4 \times 5 = 60 \text{ cm}^3 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-e0ad8747f9e4055b967fc774451f7e1f_l3.png "Rendered by QuickLaTeX.com")
Thus, the rectangular prism has a surface area of 94 square centimeters and a volume of 60 cubic centimeters.
3. Cylinder
- Surface Area: The surface area of a cylinder with radius
and height 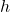is calculated using the formula:
![\[ A = 2\pi r^2 + 2\pi rh \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-cdc9c968008a744f5ee338f1359be96d_l3.png "Rendered by QuickLaTeX.com")
The first term represents the area of the two circular bases, and the second term represents the lateral surface area.
- Volume: The volume 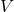of a cylinder is given by:
![\[ V = \pi r^2 h \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-2cb66985b402f3894fb120bfbf53fc59_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
Consider a cylinder with a radius of 3 cm and a height of 5 cm. To find the surface area:
![\[ A = 2\pi(3^2) + 2\pi(3)(5) = 2\pi(9) + 30\pi = 18\pi + 30\pi = 48\pi \approx 150.8 \text{ cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-b18ae0b17d7dd9da944d659b3c3e2345_l3.png "Rendered by QuickLaTeX.com")
To find the volume:
![\[ V = \pi(3^2)(5) = \pi(9)(5) = 45\pi \approx 141.4 \text{ cm}^3 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-2676989043947f5a2157365e8a6451a5_l3.png "Rendered by QuickLaTeX.com")
Thus, the cylinder has a surface area of approximately 150.8 square centimeters and a volume of approximately 141.4 cubic centimeters.
4. Sphere
- Surface Area: The surface area of a sphere with radius is calculated using the formula:
![\[ A = 4\pi r^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-dd7f001f5811b76296aad73d47e41966_l3.png "Rendered by QuickLaTeX.com")
- Volume: The volume 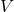of a sphere is given by:
![\[ V = \frac{4}{3}\pi r^3 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-22cbdc9f0aaf9a266021c09f3a293946_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
Consider a sphere with a radius of 4 cm. To find the surface area:
![\[ A = 4\pi(4^2) = 4\pi(16) = 64\pi \approx 201.1 \text{ cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-2e62ed0ff425928a26e96ec941169f23_l3.png "Rendered by QuickLaTeX.com")
To find the volume:
![\[ V = \frac{4}{3}\pi(4^3) = \frac{4}{3}\pi(64) = \frac{256}{3}\pi \approx 268.1 \text{ cm}^3 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-1818db675eba97fc0de2daf90a775744_l3.png "Rendered by QuickLaTeX.com")
Thus, the sphere has a surface area of approximately 201.1 square centimeters and a volume of approximately 268.1 cubic centimeters.
5. Cone
- Surface Area: The surface area of a cone with radius and height 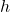is calculated using the formula:
![\[ A = \pi r^2 + \pi r l \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-2fddb2692629eb9ee3a9a7fc7c54bca9_l3.png "Rendered by QuickLaTeX.com")
where is the slant height of the cone, calculated as 
.
- Volume: The volume 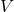of a cone is given by:
![\[ V = \frac{1}{3}\pi r^2 h \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d7d4c17a68a0d8cbb61c411db53ffe13_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
Consider a cone with a radius of 3 cm and a height of 4 cm. First, calculate the slant height:
![\[ l = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-5f8da668fc0766784a7a352fcde767f1_l3.png "Rendered by QuickLaTeX.com")
Now, to find the surface area:
![\[ A = \pi(3^2) + \pi(3)(5) = 9\pi + 15\pi = 24\pi \approx 75.4 \text{ cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-3f6011b20cdf6d739fd60ad1d84b0e03_l3.png "Rendered by QuickLaTeX.com")
To find the volume:
![\[ V = \frac{1}{3}\pi(3^2)(4) = \frac{1}{3}\pi(9)(4) = 12\pi \approx 37.7 \text{ cm}^3 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-08a3cb6200400e51ed2eb1605184242c_l3.png "Rendered by QuickLaTeX.com")
Thus, the cone has a surface area of approximately 75.4 square centimeters and a volume of approximately 37.7 cubic centimeters.
Applications of Surface Area and Volume
Understanding surface area and volume has numerous practical applications across various fields:
1. Architecture and Construction: Architects and engineers use surface area and volume calculations to design buildings, ensuring that materials are used efficiently and that structures are stable.
Illustrative Explanation
When designing a water tank, engineers must calculate the volume to ensure it can hold the required amount of water while also considering the surface area for materials needed for construction.
2. Manufacturing: In manufacturing, surface area calculations are crucial for processes such as coating, painting, and packaging, where the amount of material needed depends on the surface area of the object.
Illustrative Explanation
A company producing cans must calculate the surface area of each can to determine how much paint is needed for the exterior coating.
3. Science and Medicine: In fields such as biology and chemistry, surface area and volume are important for understanding processes like diffusion, where the rate of exchange is influenced by the surface area available.
Illustrative Explanation
In drug delivery systems, the surface area of nanoparticles can affect how quickly a drug is absorbed in the body, making surface area calculations critical for effective treatment.
4. Everyday Life: Surface area and volume concepts are relevant in everyday situations, such as cooking, where understanding the volume of containers can help in measuring ingredients accurately.
Illustrative Explanation
When baking, knowing the volume of a mixing bowl can help determine how much batter it can hold, ensuring that the recipe is followed correctly.
Conclusion
In conclusion, surface area and volume are essential concepts in geometry that describe the size and space occupied by three-dimensional objects. Understanding how to calculate surface area and volume for various geometric shapes is crucial for applications in architecture, manufacturing, science, and everyday life. By mastering these concepts, individuals can make informed decisions in a wide range of fields, from engineering to cooking. The ability to visualize and calculate surface area and volume enhances our understanding of the physical world and equips us with valuable skills for practical problem-solving.