Understanding the Surface Area of a Hemisphere: A Comprehensive Guide

The concept of surface area is fundamental in geometry, particularly when dealing with three-dimensional shapes. A hemisphere, which is half of a sphere, presents unique characteristics and applications in various fields, including mathematics, engineering, and architecture. This article will provide a detailed exploration of the surface area of a hemisphere, including its definition, formula derivation, illustrative examples, and practical applications.

1. Definition of a Hemisphere

A hemisphere is defined as half of a sphere, created by slicing the sphere along a plane that passes through its center. It consists of two main parts:

Curved Surface Area: The area of the curved surface that forms the outer part of the hemisphere.
Base Area: The area of the flat circular base that forms the bottom of the hemisphere.

The combination of these two areas gives us the total surface area of the hemisphere.

2. Formula for the Surface Area of a Hemisphere

To calculate the surface area of a hemisphere, we need to derive the formulas for both the curved surface area and the base area.

a. Curved Surface Area

The curved surface area (CSA) of a hemisphere can be derived from the formula for the surface area of a sphere. The surface area $A$ of a sphere is given by:

$A = 4\pi r^2$

where $r$ is the radius of the sphere. Since a hemisphere is half of a sphere, the curved surface area of the hemisphere is half of the total surface area of the sphere:

$\text{Curved Surface Area (CSA)} = \frac{1}{2} \times 4\pi r^2 = 2\pi r^2$

b. Base Area

The base of the hemisphere is a circle with a radius $r$ . The area $A$ of a circle is given by the formula:

$A = \pi r^2$

Thus, the base area of the hemisphere is:

$\text{Base Area} = \pi r^2$

c. Total Surface Area

The total surface area (TSA) of a hemisphere is the sum of the curved surface area and the base area:

$\text{Total Surface Area (TSA)} = \text{Curved Surface Area} + \text{Base Area}$

Substituting the formulas we derived:

$\text{Total Surface Area} = 2\pi r^2 + \pi r^2 = 3\pi r^2$

Thus, the formula for the total surface area of a hemisphere is:

$\text{Total Surface Area} = 3\pi r^2$

3. Illustrative Example

To solidify our understanding, let’s work through an example of calculating the surface area of a hemisphere.

Example: Calculate the total surface area of a hemisphere with a radius of 5 cm.

Step 1: Identify the radius.

Given: $r = 5 \, \text{cm}$

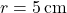
Step 2: Substitute the radius into the total surface area formula.

$\text{Total Surface Area} = 3\pi r^2 = 3\pi (5)^2$

Step 3: Calculate $r^2$ .

$(5)^2 = 25$

Step 4: Substitute back into the formula.

$\text{Total Surface Area} = 3\pi (25) = 75\pi$

Step 5: Approximate the value using $\pi \approx 3.14$ .

$\text{Total Surface Area} \approx 75 \times 3.14 \approx 235.5 \, \text{cm}^2$

Thus, the total surface area of the hemisphere is approximately $235.5 \, \text{cm}^2$ .

4. Practical Applications of the Surface Area of a Hemisphere

Understanding the surface area of a hemisphere has several practical applications across various fields:

Engineering and Architecture: Hemispherical shapes are often used in the design of domes, tanks, and other structures. Calculating the surface area is essential for determining the amount of material needed for construction and for insulation purposes.
Manufacturing: In industries that produce spherical or hemispherical objects, such as containers, bowls, and caps, knowing the surface area helps in optimizing material usage and cost.
Physics and Astronomy: The concept of hemispheres is used in various physical models, including the study of celestial bodies and their gravitational fields. Understanding surface area can aid in calculations related to light absorption and radiation.
Art and Design: In sculpture and design, hemispherical shapes are often used for aesthetic purposes. Artists and designers may need to calculate surface areas for painting, coating, or finishing surfaces.

5. Conclusion

The surface area of a hemisphere is a fundamental concept in geometry that has wide-ranging applications in various fields. By understanding the derivation of the formulas for curved surface area, base area, and total surface area, individuals can effectively calculate and apply these concepts in real-world scenarios. The formula $3\pi r^2$ provides a straightforward method for determining the total surface area of a hemisphere, making it an essential tool for students, engineers, architects, and professionals alike. Whether in theoretical mathematics or practical applications, the study of the surface area of a hemisphere enhances our understanding of three-dimensional shapes and their properties.

Blog.Pengayaan.Com