Three-Dimensional Shapes: A Comprehensive Exploration

Three-dimensional shapes, also known as 3D shapes, are geometric figures that have depth in addition to height and width. Unlike two-dimensional shapes, which exist only on a flat plane, three-dimensional shapes occupy space and can be perceived from multiple angles. This article aims to provide an exhaustive overview of three-dimensional shapes, detailing their definitions, types, properties, formulas, applications, and illustrative explanations for each concept.

1. Definition of Three-Dimensional Shapes

1.1. What are Three-Dimensional Shapes?

A three-dimensional shape is defined as a solid object that has three dimensions: length, width, and height. These shapes can be described using various geometric properties, including faces, edges, and vertices.

Faces: The flat surfaces that make up the shape.
Edges: The line segments where two faces meet.
Vertices: The points where edges meet.

Illustrative Explanation: Consider a cube, which is a common three-dimensional shape. A cube has six square faces, twelve edges, and eight vertices. Each face is a flat surface, while the edges are the lines connecting the corners (vertices) of the cube.

2. Types of Three-Dimensional Shapes

Three-dimensional shapes can be classified into several categories based on their properties. Here are some of the most common types:

2.1. Polyhedra

Polyhedra are three-dimensional shapes with flat polygonal faces. They are characterized by having a finite number of faces, edges, and vertices. Polyhedra can be further classified into regular and irregular polyhedra.

Regular Polyhedra: All faces are congruent regular polygons, and the same number of faces meet at each vertex. The five regular polyhedra are known as the Platonic solids: tetrahedron, cube, octahedron, dodecahedron, and icosahedron.

Illustrative Explanation: A cube is a regular polyhedron with six square faces, twelve edges, and eight vertices. Each face is identical, and the angles between the faces are the same.

Irregular Polyhedra: These have faces that are not all congruent or regular. An example is a rectangular prism, which has rectangular faces but is not a regular polyhedron.

2.2. Prisms

A prism is a type of polyhedron that has two parallel, congruent bases connected by rectangular lateral faces. The shape of the base determines the type of prism.

Triangular Prism: Has triangular bases and three rectangular lateral faces.
Rectangular Prism: Has rectangular bases and four rectangular lateral faces.

Illustrative Explanation: A triangular prism can be visualized as a tent with triangular ends. The two triangular bases are parallel, and the three rectangular faces connect the corresponding sides of the triangles.

2.3. Pyramids

A pyramid is a polyhedron with a polygonal base and triangular faces that converge at a single point called the apex. The type of pyramid is determined by the shape of its base.

Square Pyramid: Has a square base and four triangular faces.
Triangular Pyramid (Tetrahedron): Has a triangular base and three triangular faces.

Illustrative Explanation: A square pyramid resembles a pyramid found in ancient Egypt. The square base is at the bottom, and the four triangular faces meet at the apex above the center of the base.

2.4. Cylinders

A cylinder is a three-dimensional shape with two parallel circular bases connected by a curved surface. The height of the cylinder is the perpendicular distance between the bases.

Illustrative Explanation: A common example of a cylinder is a soda can. The circular top and bottom are the bases, while the curved surface that wraps around connects them.

2.5. Cones

A cone is a three-dimensional shape with a circular base and a single vertex (the apex) that is not in the same plane as the base. The curved surface connects the base to the apex.

Illustrative Explanation: An ice cream cone is a familiar example. The circular base is the bottom of the cone, while the sides taper up to a point at the top.

2.6. Spheres

A sphere is a perfectly round three-dimensional shape where every point on the surface is equidistant from the center. It has no edges or vertices.

Illustrative Explanation: A basketball is a practical example of a sphere. No matter where you measure from the center, the distance to the surface remains constant.

3. Properties of Three-Dimensional Shapes

3.1. Faces, Edges, and Vertices

Each type of three-dimensional shape has a specific number of faces, edges, and vertices. Understanding these properties is crucial for identifying and classifying shapes.

Cube: 6 faces, 12 edges, 8 vertices.
Triangular Prism: 5 faces, 9 edges, 6 vertices.
Square Pyramid: 5 faces, 8 edges, 5 vertices.
Cylinder: 3 faces (2 circular bases and 1 curved surface), 0 edges, 0 vertices.
Cone: 2 faces (1 circular base and 1 curved surface), 1 edge, 1 vertex.
Sphere: 1 curved surface, 0 edges, 0 vertices.

3.2. Surface Area and Volume

The surface area and volume of three-dimensional shapes are important measurements that describe their size and capacity.

Surface Area: The total area of all the faces of a three-dimensional shape.
Volume: The amount of space occupied by the shape.

Formulas:

Cube:

– Surface Area: $6s^2$ (where $s$ is the length of a side)
– Volume: $s^3$

Rectangular Prism:

– Surface Area: $2(lw + lh + wh)$ (where $l$ , $w$ , and $h$ are length, width, and height)
– Volume: $l \times w \times h$

Cylinder:

– Surface Area: $2\pi r(h + r)$ (where $r$ is the radius and $h$ is the height)
– Volume: $\pi r^2 h$

Cone:

– Surface Area: $\pi r(r + l)$ (where $l$ is the slant height)
– Volume: $\frac{1}{3}\pi r^2 h$

Sphere:

– Surface Area: $4\pi r^2$
– Volume: $\frac{4}{3}\pi r^3$

Illustrative Explanation: For a cube with a side length of $3 \, \text{cm}$ :

Surface Area: $6 \times (3^2) = 6 \times 9 = 54 \, \text{cm}^2$
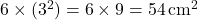
Volume: $3^3 = 27 \, \text{cm}^3$

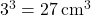
4. Applications of Three-Dimensional Shapes

4.1. Architecture and Engineering

Three-dimensional shapes are fundamental in architecture and engineering. Buildings, bridges, and other structures are designed using various 3D shapes to ensure stability and functionality.

Illustrative Explanation: An architect may use cylindrical columns to support a roof, while the overall structure may incorporate rectangular prisms for walls and pyramids for roofs.

4.2. Manufacturing and Design

In manufacturing, three-dimensional shapes are essential for creating products. Designers use 3D modeling software to visualize and prototype items before production.

Illustrative Explanation: A car manufacturer may design the body of a car as a combination of various 3D shapes, such as cylinders for the wheels and rectangular prisms for the chassis.

4.3. Computer Graphics and Animation

Three-dimensional shapes are crucial in computer graphics and animation. Artists create 3D models for video games, movies, and simulations, allowing for realistic representations of objects.

Illustrative Explanation: In a video game, characters and environments are often modeled as 3D shapes, enabling players to interact with them from different angles and perspectives.

4.4. Education and Learning

Three-dimensional shapes are used in education to teach students about geometry, spatial reasoning, and measurement. Hands-on activities with physical models help students understand the properties of 3D shapes.

Illustrative Explanation: Teachers may use blocks or clay to help students visualize and create different three-dimensional shapes, reinforcing their understanding of concepts like volume and surface area.

5. Limitations of Three-Dimensional Shapes

5.1. Complexity in Visualization

Understanding and visualizing three-dimensional shapes can be challenging, especially for individuals who are more accustomed to two-dimensional representations. This complexity can lead to difficulties in spatial reasoning.

5.2. Measurement Challenges

Measuring the dimensions of three-dimensional shapes accurately can be more complicated than measuring two-dimensional shapes. For example, determining the height of a cone or the slant height of a pyramid requires careful consideration.

5.3. Material Constraints

In practical applications, the choice of materials can limit the design and construction of three-dimensional shapes. For instance, certain shapes may be difficult to construct with specific materials due to their structural properties.

Conclusion

In conclusion, three-dimensional shapes are a vital aspect of geometry, characterized by their length, width, and height. They can be classified into various types, including polyhedra, prisms, pyramids, cylinders, cones, and spheres, each with unique properties and applications. Understanding three-dimensional shapes involves recognizing their faces, edges, vertices, surface area, and volume. These shapes play a crucial role in architecture, engineering, manufacturing, computer graphics, and education. As we continue to explore the rich world of geometry, the study of three-dimensional shapes will remain an essential area of research and application, inspiring curiosity and discovery in the realm of spatial understanding. Whether in theoretical mathematics or practical applications, three-dimensional shapes serve as a cornerstone for understanding the relationships between dimensions, measurements, and real-world objects, making them an essential topic for anyone interested in geometry.

Blog.Pengayaan.Com