A trapezium, also known as a trapezoid in American English, is a fundamental geometric shape that plays a significant role in various fields of mathematics, architecture, engineering, and design. This article will provide a detailed exploration of trapeziums, including their definition, properties, types, area calculation, and applications, along with illustrative explanations to enhance understanding.
Definition of a Trapezium
A trapezium is defined as a four-sided polygon (quadrilateral) that has at least one pair of parallel sides. The parallel sides are referred to as the “bases” of the trapezium, while the other two sides are called the “legs.” The length of the bases can be different, and the angles between the bases and the legs can vary, leading to different types of trapeziums.
Mathematically, a trapezium can be represented as follows:
- Let
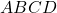be a trapezium where 
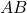and 
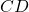are the parallel sides (bases), and 
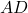and 
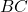are the non-parallel sides (legs).
Properties of Trapezium
1. Parallel Sides: The defining characteristic of a trapezium is that it has at least one pair of parallel sides. This property leads to several other geometric properties.
2. Sum of Angles: The sum of the interior angles of any quadrilateral, including a trapezium, is always 
. This can be expressed as:
![\[ \angle A + \angle B + \angle C + \angle D = 360^\circ \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-fb55c65ee11d402580905076661b0263_l3.png "Rendered by QuickLaTeX.com")
3. Base Angles: In an isosceles trapezium (a special type of trapezium), the angles adjacent to each base are equal. For example, in trapezium , if is parallel to , then:
![\[ \angle A = \angle B \quad \text{and} \quad \angle C = \angle D \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-cdfa766d24b14e81568194d78c6517ae_l3.png "Rendered by QuickLaTeX.com")
4. Height: The height (or altitude) of a trapezium is the perpendicular distance between the two bases. This height is crucial for calculating the area of the trapezium.
5. Midsegment: The midsegment (or median) of a trapezium is a line segment that connects the midpoints of the legs. The length of the midsegment is the average of the lengths of the two bases:
![\[ \text{Midsegment} = \frac{AB + CD}{2} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-738ef4a4339c50ccc1acd61cdbc588dd_l3.png "Rendered by QuickLaTeX.com")
Types of Trapezium
Trapeziums can be classified into different types based on the properties of their sides and angles:
1. General Trapezium: A trapezium with no specific properties regarding the lengths of the legs or the angles. The bases can be of different lengths, and the legs can be of different lengths as well.
Illustrative Example:
![\[ A = \begin{pmatrix} 1 & 2 \\ 4 & 2 \\ 3 & 5 \\ 0 & 5 \end{pmatrix} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d851c520989ce18f31459ff6d57576c3_l3.png "Rendered by QuickLaTeX.com")
In this trapezium, and are parallel, but the lengths of and are not equal.
2. Isosceles Trapezium: A trapezium where the non-parallel sides (legs) are of equal length. In an isosceles trapezium, the base angles are also equal.
Illustrative Example:
![\[ A = \begin{pmatrix} 1 & 2 \\ 4 & 2 \\ 3 & 5 \\ 2 & 5 \end{pmatrix} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-8169e90103e4f64c3b8697cbd2f5ffc7_l3.png "Rendered by QuickLaTeX.com")
Here, 
and 
.
3. Right Trapezium: A trapezium that has at least two right angles. This means that one leg is perpendicular to the bases.
Illustrative Example:
![\[ A = \begin{pmatrix} 1 & 2 \\ 4 & 2 \\ 4 & 5 \\ 1 & 5 \end{pmatrix} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d452ade0b3d9286a82a3bb962ab3aa68_l3.png "Rendered by QuickLaTeX.com")
In this trapezium, 
and 
are right angles.
Area of a Trapezium
The area 
of a trapezium can be calculated using the following formula:
![\[ A = \frac{1}{2} \times (b_1 + b_2) \times h \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-127252d241cc8b68d147d6d2465c577a_l3.png "Rendered by QuickLaTeX.com")
Where:
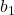and 
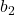are the lengths of the two parallel sides (bases).
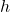is the height (the perpendicular distance between the bases).
Illustrative Example:
Consider a trapezium with bases 
units and 
units, and a height of 
units. The area can be calculated as follows:
![\[ A = \frac{1}{2} \times (8 + 5) \times 4 = \frac{1}{2} \times 13 \times 4 = 26 \text{ square units} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ab70a0ea12996d27e848a5fff000022a_l3.png "Rendered by QuickLaTeX.com")
Applications of Trapezium
Trapeziums have various applications in different fields:
1. Architecture and Engineering: Trapeziums are often used in architectural designs, such as roofs and bridges, where the shape provides structural stability.
2. Land Surveying: In land surveying, trapeziums are used to calculate areas of irregular plots of land, especially when the land can be divided into trapezoidal sections.
3. Graphic Design: Trapeziums are used in graphic design and art to create visually appealing shapes and patterns.
4. Mathematics: Trapeziums are studied in geometry to understand properties of quadrilaterals and to solve problems related to area and perimeter.
5. Physics: In physics, trapeziums can represent certain shapes in mechanics, such as inclined planes or ramps.
Conclusion
In conclusion, a trapezium is a versatile geometric shape characterized by having at least one pair of parallel sides. Understanding the properties, types, area calculation, and applications of trapeziums is essential for solving various mathematical problems and for practical applications in fields such as architecture, engineering, and design. Through detailed explanations and illustrative examples, we can appreciate the significance of trapeziums in both theoretical and practical contexts, showcasing their importance in the broader landscape of mathematics. Whether calculating areas, designing structures, or analyzing land plots, trapeziums remain a cornerstone of geometric understanding and application.