Trigonometry Table: A Comprehensive Overview

Trigonometry is a branch of mathematics that studies the relationships between the angles and sides of triangles, particularly right triangles. It has applications in various fields, including physics, engineering, astronomy, and architecture. A trigonometry table is a valuable tool that provides the values of trigonometric functions for specific angles, making it easier to solve problems involving triangles and periodic phenomena. This article will explore the trigonometric functions, the construction of a trigonometry table, and illustrative explanations of each concept.

Understanding Trigonometric Functions

Trigonometric functions relate the angles of a triangle to the ratios of its sides. The primary trigonometric functions are:

1. Sine (sin)

The sine of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the hypotenuse.

$\text{sin}(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}$

Illustrative Explanation: In a right triangle with an angle 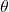$\theta$ , if the length of the side opposite to 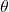$\theta$ is 3 units and the length of the hypotenuse is 5 units, then:

$\text{sin}(\theta) = \frac{3}{5} = 0.6$

2. Cosine (cos)

The cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse.

$\text{cos}(\theta) = \frac{\text{Adjacent}}{\text{Hypotenuse}}$

Illustrative Explanation: In the same triangle, if the length of the side adjacent to 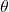$\theta$ is 4 units, then:

$\text{cos}(\theta) = \frac{4}{5} = 0.8$

3. Tangent (tan)

The tangent of an angle is defined as the ratio of the length of the opposite side to the length of the adjacent side.

$\text{tan}(\theta) = \frac{\text{Opposite}}{\text{Adjacent}}$

Illustrative Explanation: Using the previous triangle, the tangent of 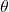$\theta$ would be:

$\text{tan}(\theta) = \frac{3}{4} = 0.75$

4. Cosecant (csc)

The cosecant is the reciprocal of the sine function.

$\text{csc}(\theta) = \frac{1}{\text{sin}(\theta)} = \frac{\text{Hypotenuse}}{\text{Opposite}}$

Illustrative Explanation: For our triangle, since $\text{sin}(\theta) = 0.6$ :

$\text{csc}(\theta) = \frac{1}{0.6} \approx 1.67$

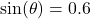5. Secant (sec)

The secant is the reciprocal of the cosine function.

$\text{sec}(\theta) = \frac{1}{\text{cos}(\theta)} = \frac{\text{Hypotenuse}}{\text{Adjacent}}$

Illustrative Explanation: For our triangle, since $\text{cos}(\theta) = 0.8$ :

$\text{sec}(\theta) = \frac{1}{0.8} = 1.25$

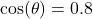6. Cotangent (cot)

The cotangent is the reciprocal of the tangent function.

$\text{cot}(\theta) = \frac{1}{\text{tan}(\theta)} = \frac{\text{Adjacent}}{\text{Opposite}}$

Illustrative Explanation: For our triangle, since $\text{tan}(\theta) = 0.75$ :

$\text{cot}(\theta) = \frac{1}{0.75} \approx 1.33$

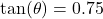Constructing a Trigonometry Table

A trigonometry table lists the values of the trigonometric functions for specific angles, typically in degrees and radians. The most common angles used in trigonometry tables are 0°, 30°, 45°, 60°, and 90° (or their radian equivalents: 0, $\frac{\pi}{6}$ , $\frac{\pi}{4}$ , $\frac{\pi}{3}$ , and $\frac{\pi}{2}$ ).

Example of a Trigonometry Table

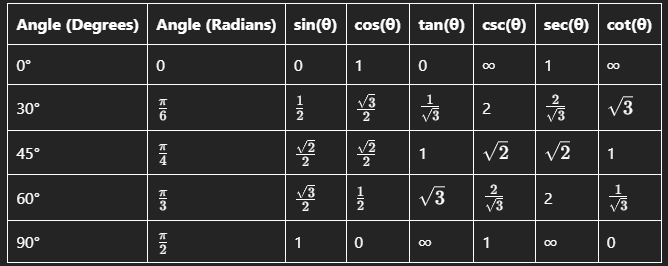
Illustrative Explanation of the Table

0° (0 radians):

– $\text{sin}(0) = 0$ means there is no vertical height.
– $\text{cos}(0) = 1$ indicates the maximum horizontal distance.
– $\text{tan}(0) = 0$ shows no slope.

30° ( 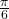$\frac{\pi}{6}$ radians):

– $\text{sin}(30°) = \frac{1}{2}$ indicates that the opposite side is half the hypotenuse.
– $\text{cos}(30°) = \frac{\sqrt{3}}{2}$ shows that the adjacent side is approximately 0.866 times the hypotenuse.
– $\text{tan}(30°) = \frac{1}{\sqrt{3}}$ indicates a gentle slope.

45° ( 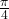$\frac{\pi}{4}$ radians):

– Both sine and cosine are equal, indicating an isosceles right triangle where the opposite and adjacent sides are equal.
– $\text{tan}(45°) = 1$ shows a 45-degree slope.

60° ( 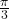$\frac{\pi}{3}$ radians):

– $\text{sin}(60°) = \frac{\sqrt{3}}{2}$ indicates a higher opposite side compared to the adjacent side.
– $\text{tan}(60°) = \sqrt{3}$ shows a steeper slope.

90° ( 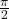$\frac{\pi}{2}$ radians):

– $\text{sin}(90°) = 1$ indicates the maximum height.
– $\text{cos}(90°) = 0$ shows no horizontal distance.
– $\text{tan}(90°)$ is undefined, as it represents a vertical line.

Applications of Trigonometry Tables

Trigonometry tables are widely used in various fields:

1. Engineering and Physics

Engineers and physicists use trigonometric functions to analyze forces, waves, and oscillations. Trigonometry tables help in quickly finding the values needed for calculations.

2. Architecture

Architects use trigonometry to calculate heights, distances, and angles in building designs. Trigonometric tables assist in ensuring structural integrity and aesthetic proportions.

3. Navigation

In navigation, trigonometry is used to determine positions and distances. Trigonometric tables help navigators calculate angles and bearings.

4. Computer Graphics

In computer graphics, trigonometric functions are used to create realistic animations and models. Trigonometry tables aid in rendering angles and transformations.

Conclusion

A trigonometry table is an invaluable resource that provides the values of trigonometric functions for specific angles. Understanding the fundamental trigonometric functions—sine, cosine, tangent, cosecant, secant, and cotangent—along with their properties and applications, is essential for solving problems in mathematics, physics, engineering, and many other fields. By utilizing trigonometry tables, students and professionals can efficiently access the necessary values to perform calculations and analyze relationships in triangles and periodic phenomena. As we continue to explore the world of trigonometry, the trigonometry table will remain a vital tool in our mathematical toolkit, enabling us to navigate the complexities of angles and distances effectively.

Blog.Pengayaan.Com