In mathematics, a function is a fundamental concept that describes a relationship between a set of inputs and a set of possible outputs. Each input is related to exactly one output, which makes functions a crucial building block in various fields, including algebra, calculus, and computer science. Understanding the different types of functions is essential for solving mathematical problems and applying these concepts in real-world scenarios. This article aims to provide an exhaustive overview of the various types of functions, detailing their definitions, properties, and illustrative explanations for each concept.
1. Definition of a Function
A function ![]() can be defined as a relation between a set of inputs (domain) and a set of outputs (range) such that each input is associated with exactly one output. Mathematically, this can be expressed as:
can be defined as a relation between a set of inputs (domain) and a set of outputs (range) such that each input is associated with exactly one output. Mathematically, this can be expressed as:
![]()
Where:
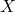 is the domain (the set of all possible inputs),
is the domain (the set of all possible inputs),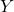 is the codomain (the set of all possible outputs).
is the codomain (the set of all possible outputs).- Illustrative Explanation: Imagine a vending machine. You insert a specific amount of money (input), select a button (input), and receive a specific snack (output). Each button corresponds to one snack, illustrating the concept of a function where each input has a unique output.
2. Types of Functions
2.1. Linear Functions
A linear function is a function that can be expressed in the form:
![]()
Where:
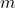 is the slope of the line,
is the slope of the line,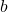 is the y-intercept (the point where the line crosses the y-axis).
is the y-intercept (the point where the line crosses the y-axis).
Linear functions produce a straight line when graphed.
- Illustrative Explanation: Consider the relationship between the distance traveled and time at a constant speed. If you drive at a speed of 60 miles per hour, the distance
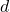 can be expressed as
can be expressed as 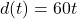 . This relationship is linear, and if you graph it, you will see a straight line.
. This relationship is linear, and if you graph it, you will see a straight line.
2.2. Quadratic Functions
A quadratic function is a polynomial function of degree 2, expressed in the form:
![]()
Where:
 ,
, 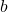 , and
, and  are constants, and
are constants, and 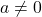 .
.
The graph of a quadratic function is a parabola, which can open upwards or downwards depending on the sign of ![]() .
.
- Illustrative Explanation: Imagine throwing a ball into the air. The height
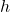 of the ball over time can be modeled by a quadratic function, such as
of the ball over time can be modeled by a quadratic function, such as 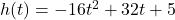 . The graph of this function will form a parabola, illustrating the ball’s rise and fall.
. The graph of this function will form a parabola, illustrating the ball’s rise and fall.
2.3. Polynomial Functions
A polynomial function is a function that can be expressed in the form:
![]()
Where:
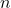 is a non-negative integer (the degree of the polynomial),
is a non-negative integer (the degree of the polynomial),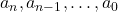 are constants.
are constants.
Polynomial functions can have various shapes depending on their degree.
- Illustrative Explanation: Consider the function
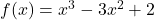 . This cubic polynomial can have one or more turning points, and its graph will have a characteristic “S” shape, demonstrating how polynomial functions can vary widely in appearance.
. This cubic polynomial can have one or more turning points, and its graph will have a characteristic “S” shape, demonstrating how polynomial functions can vary widely in appearance.
2.4. Rational Functions
A rational function is a function that can be expressed as the ratio of two polynomials:
![]()
Where ![]() and
and ![]() are polynomials, and
are polynomials, and ![]() .
.
Rational functions can exhibit asymptotic behavior, where the graph approaches a line but never touches it.
- Illustrative Explanation: Consider the function
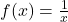 . As
. As 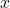 approaches 0, the function approaches infinity, creating a vertical asymptote. The graph will never touch the y-axis, illustrating the unique behavior of rational functions.
approaches 0, the function approaches infinity, creating a vertical asymptote. The graph will never touch the y-axis, illustrating the unique behavior of rational functions.
2.5. Exponential Functions
An exponential function is a function of the form:
![]()
Where:
 is a constant,
is a constant,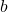 is a positive real number (the base of the exponential).
is a positive real number (the base of the exponential).
Exponential functions grow rapidly and are characterized by their constant percentage growth rate.
- Illustrative Explanation: Consider the growth of a bank account with compound interest. If you invest $100 at an interest rate of 5% compounded annually, the amount
 in the account after
in the account after 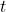 years can be modeled by the function
years can be modeled by the function 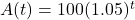 . The graph of this function will show rapid growth as time increases.
. The graph of this function will show rapid growth as time increases.
2.6. Logarithmic Functions
A logarithmic function is the inverse of an exponential function and can be expressed as:
![]()
Where:
 and
and 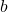 are constants,
are constants, is the base of the logarithm.
is the base of the logarithm.
Logarithmic functions grow slowly compared to exponential functions.
- Illustrative Explanation: If you measure the intensity of an earthquake using the Richter scale, the scale is logarithmic. An earthquake that measures 6.0 on the Richter scale is ten times more intense than one that measures 5.0. This illustrates how logarithmic functions can represent phenomena that grow at a decreasing rate.
2.7. Trigonometric Functions
Trigonometric functions relate angles to the ratios of sides in right triangles and are periodic functions. The primary trigonometric functions include sine, cosine, and tangent, expressed as:
These functions are essential in modeling periodic phenomena such as sound waves and circular motion.
- Illustrative Explanation: Consider the motion of a Ferris wheel. As a passenger moves around the wheel, their height above the ground can be modeled using the sine function. The height will oscillate between a maximum and minimum value, illustrating the periodic nature of trigonometric functions.
2.8. Piecewise Functions
A piecewise function is defined by different expressions for different intervals of the input variable. It can be expressed as:
![Rendered by QuickLaTeX.com \[ f(x) = \begin{cases} x^2 & \text{if } x < 0 \\ x + 1 & \text{if } x \geq 0 \end{cases} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-01640be15e4b59423910967c74a7d3c0_l3.png)
Piecewise functions can model situations where a rule changes based on the input value.
- Illustrative Explanation: Imagine a toll road where the toll is $2 for cars under 5 feet tall and $5 for cars over 5 feet tall. The toll function can be represented as a piecewise function, illustrating how the cost changes based on the height of the vehicle.
2.9. Implicit Functions
An implicit function is defined by an equation that relates the dependent and independent variables without explicitly solving for one variable in terms of the other. For example, the equation of a circle:
![]()
defines ![]() implicitly in terms of
implicitly in terms of ![]() .
.
- Illustrative Explanation: Consider the equation of a circle centered at the origin. While you can find the explicit function for the upper half of the circle as
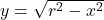 , the implicit form captures both the upper and lower halves of the circle without needing to solve for
, the implicit form captures both the upper and lower halves of the circle without needing to solve for  .
.
Conclusion
In conclusion, functions are a fundamental concept in mathematics, and understanding the various types of functions is essential for solving problems and applying mathematical principles in real-world scenarios. From linear and quadratic functions to exponential and logarithmic functions, each type has unique properties and applications. By exploring these different types of functions, we gain valuable insights into the relationships between variables and the behavior of mathematical models. As we continue to study mathematics, the knowledge of functions will remain a key component of our understanding of the world around us.