Types of Triangles: A Comprehensive Exploration

Triangles are fundamental geometric shapes that consist of three sides, three angles, and three vertices. They are one of the simplest forms of polygons and serve as the building blocks for more complex geometric figures. Understanding the different types of triangles is essential in various fields, including mathematics, architecture, engineering, and art. This article aims to provide an exhaustive overview of the types of triangles, including their definitions, classifications, properties, and illustrative explanations for each concept.

1. Classification of Triangles

Triangles can be classified based on two primary criteria: the lengths of their sides and the measures of their angles. Each classification provides unique insights into the properties and characteristics of the triangle.

1.1. Classification by Sides

Triangles can be classified into three types based on the lengths of their sides:

1.1.1. Equilateral Triangle

An equilateral triangle has all three sides of equal length. Consequently, all three angles are also equal, each measuring $60^\circ$ .

Illustrative Explanation: Imagine a triangle where each side measures $5$ units. Since all sides are equal, the triangle is equilateral. If you were to measure each angle, you would find that they all measure $60^\circ$ .

1.1.2. Isosceles Triangle

An isosceles triangle has at least two sides of equal length. The angles opposite the equal sides are also equal.

Illustrative Explanation: Consider a triangle with two sides measuring $4$ units and the third side measuring $3$ units. This triangle is isosceles because it has two equal sides. The angles opposite the equal sides will also be equal, which can be useful in various applications, such as in construction and design.

1.1.3. Scalene Triangle

A scalene triangle has all sides of different lengths. Consequently, all three angles are also different.

Illustrative Explanation: Picture a triangle with sides measuring $3$ , $4$ , and $5$ units. This triangle is scalene because no sides are equal, and the angles will also differ from one another. Scalene triangles are often encountered in real-world applications, such as in irregular structures.

1.2. Classification by Angles

Triangles can also be classified based on the measures of their angles:

1.2.1. Acute Triangle

An acute triangle has all three angles measuring less than $90^\circ$ .

Illustrative Explanation: Imagine a triangle where each angle measures $30^\circ$ , $60^\circ$ , and $80^\circ$ . Since all angles are less than $90^\circ$ , this triangle is classified as acute. Acute triangles are often found in various designs and structures due to their sharp angles.

1.2.2. Right Triangle

A right triangle has one angle that measures exactly $90^\circ$ . The side opposite the right angle is known as the hypotenuse, and it is the longest side of the triangle.

Illustrative Explanation: Consider a triangle with angles measuring $30^\circ$ , $60^\circ$ , and $90^\circ$ . The $90^\circ$ angle makes this triangle a right triangle. Right triangles are particularly important in trigonometry and are used extensively in construction and navigation.

1.2.3. Obtuse Triangle

An obtuse triangle has one angle that measures more than $90^\circ$ . The other two angles must be acute, meaning they are less than $90^\circ$ .

Illustrative Explanation: Picture a triangle with angles measuring $120^\circ$ , $30^\circ$ , and $30^\circ$ . The $120^\circ$ angle makes this triangle obtuse. Obtuse triangles can often be seen in various artistic designs and architectural features.

2. Properties of Triangles

2.1. Sum of Angles

One of the fundamental properties of triangles is that the sum of the interior angles always equals $180^\circ$ . This property holds true for all types of triangles, regardless of their classification.

Illustrative Explanation: If you have a triangle with angles measuring $50^\circ$ , $60^\circ$ , and $70^\circ$ , you can verify that:

$50^\circ + 60^\circ + 70^\circ = 180^\circ$

2.2. Triangle Inequality Theorem

The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. This theorem is crucial for determining whether a set of three lengths can form a triangle.

Illustrative Explanation: If you have sides measuring $3$ , $4$ , and $5$ units, you can check:

$3 + 4 > 5$ (True)
$3 + 5 > 4$ (True)
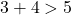$4 + 5 > 3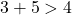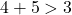$ (True)

Since all conditions are satisfied, these lengths can form a triangle.

2.3. Congruence and Similarity

Triangles can be congruent (identical in shape and size) or similar (same shape but different sizes). Congruent triangles have equal corresponding sides and angles, while similar triangles have proportional corresponding sides and equal corresponding angles.

Illustrative Explanation: If two triangles have sides measuring $3$ , $4$ , and $5$ units, they are congruent. If one triangle has sides measuring $6$ , $8$ , and $10$ units, it is similar to the first triangle because the sides are in proportion (2:1).

3. Applications of Triangles

3.1. Architecture and Engineering

Triangles are widely used in architecture and engineering due to their inherent strength and stability. Triangular shapes are often employed in trusses, bridges, and roof designs to distribute weight evenly.

Illustrative Explanation: A triangular truss in a bridge helps support the structure by distributing the load across its three sides, preventing collapse.

3.2. Art and Design

Triangles are fundamental in art and design, often used to create visually appealing compositions. Artists and designers utilize triangular shapes to guide the viewer’s eye and create balance in their work.

Illustrative Explanation: In a painting, the use of triangular shapes can lead the viewer’s gaze toward a focal point, enhancing the overall composition.

3.3. Navigation and Surveying

Triangles play a crucial role in navigation and surveying. The principles of triangulation are used to determine distances and locations based on the angles and distances between points.

Illustrative Explanation: Surveyors often use triangulation to measure large distances by creating a network of triangles, allowing them to calculate positions accurately.

3.4. Trigonometry

Triangles are the foundation of trigonometry, a branch of mathematics that studies the relationships between the angles and sides of triangles. Trigonometric functions such as sine, cosine, and tangent are based on the properties of right triangles.

Illustrative Explanation: In a right triangle, if you know one angle and one side, you can use trigonometric functions to find the lengths of the other sides and angles.

4. Limitations of Triangle Classifications

4.1. Assumption of Perfect Shapes

The classifications of triangles assume that the shapes are perfect. In reality, imperfections in measurement or construction can lead to variations that may not fit neatly into these categories.

4.2. Complexity in Real-World Applications

In real-world applications, triangles may not always conform to the ideal definitions. For example, irregular shapes may resemble triangles but do not meet the strict criteria for classification.

4.3. Measurement Errors

In practical applications, measurement errors can lead to discrepancies in determining the type of triangle. Precision in measurement is crucial for accurate classification.

Conclusion

In conclusion, triangles are fundamental geometric shapes that can be classified based on the lengths of their sides and the measures of their angles. Understanding the different types of triangles—equilateral, isosceles, scalene, acute, right, and obtuse—is essential for students and professionals in various fields. Triangles possess unique properties, such as the sum of their angles equaling $180^\circ$ and the triangle inequality theorem, which are crucial for solving geometric problems. The applications of triangles in architecture, art, navigation, and trigonometry highlight their importance in both theoretical and practical contexts. By mastering the concept of triangles, individuals can enhance their problem-solving skills and deepen their understanding of geometric relationships, paving the way for more advanced mathematical concepts and applications.

Blog.Pengayaan.Com