Momentum is a fundamental concept in physics that describes the quantity of motion an object possesses. It is a vector quantity, meaning it has both magnitude and direction. Understanding the unit of momentum is crucial for analyzing the motion of objects in various contexts, from everyday life to advanced physics. This article will delve into the definition of momentum, its mathematical representation, the unit of momentum, its significance, and illustrative explanations for each concept.
Definition of Momentum
Momentum (
) is defined as the product of an object’s mass and its velocity. It quantifies how much motion an object has and is directly related to the object’s mass and speed. The formula for momentum is given by:
![\[ p = mv \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-5ef1aafb7eb1ef1dc8ca3bb580dc8b7e_l3.png "Rendered by QuickLaTeX.com")
Where:
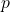- is the momentum (measured in kilograms meter per second, kg·m/s).
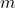is the mass of the object (measured in kilograms, kg).
is the velocity of the object (measured in meters per second, m/s).
Illustrative Explanation
To visualize momentum, consider a bowling ball and a tennis ball. If both balls are rolling towards you, the bowling ball, which has a larger mass, will have more momentum than the tennis ball, even if they are moving at the same speed. This is because momentum depends not only on how fast an object is moving (velocity) but also on how heavy it is (mass). If you were to collide with both balls, the bowling ball would have a greater impact due to its higher momentum.
Mathematical Representation of Momentum
The mathematical representation of momentum can be expressed in terms of its components. Since momentum is a vector quantity, it can be broken down into its components in a coordinate system. For example, in two dimensions, the momentum can be represented as:
![\[ \mathbf{p} = (p_x, p_y) = (mv_x, mv_y) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-74db6c48ce95263721850ea43aca782a_l3.png "Rendered by QuickLaTeX.com")
Where:
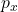and 
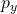are the momentum components in the x and y directions, respectively.
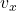and 
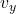are the velocity components in the x and y directions.
Illustrative Explanation
Imagine a soccer player kicking a ball. If the ball is kicked at an angle, its momentum can be analyzed in two dimensions: horizontal (x-direction) and vertical (y-direction). The total momentum of the ball is the combination of its momentum in both directions. This breakdown helps in understanding the ball’s trajectory and how it will move through the air.
Unit of Momentum
The standard unit of momentum in the International System of Units (SI) is the kilogram meter per second (kg·m/s). This unit arises from the definition of momentum as the product of mass (in kilograms) and velocity (in meters per second).
Illustrative Explanation
To understand the unit of momentum, consider a car with a mass of 1,000 kg traveling at a speed of 20 m/s. The momentum of the car can be calculated as:
![\[ p = mv = (1000 \, \text{kg})(20 \, \text{m/s}) = 20,000 \, \text{kg·m/s} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f2463e95ae7438aaf21542f0b9f109a2_l3.png "Rendered by QuickLaTeX.com")
This means the car has a momentum of 20,000 kg·m/s, indicating how much motion it possesses. If you were to compare this to a smaller vehicle, say a motorcycle with a mass of 200 kg traveling at the same speed, its momentum would be:
![\[ p = (200 \, \text{kg})(20 \, \text{m/s}) = 4,000 \, \text{kg·m/s} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-63506cfb40d958d6b90702d0580e8a17_l3.png "Rendered by QuickLaTeX.com")
The motorcycle has less momentum than the car, reflecting its lower mass.
Significance of Momentum
Momentum is significant in various areas of physics and engineering for several reasons:
1. Conservation of Momentum: One of the fundamental principles in physics is the conservation of momentum, which states that in a closed system (where no external forces act), the total momentum before an event (like a collision) is equal to the total momentum after the event. This principle is crucial for analyzing collisions and interactions between objects.
Illustrative Explanation
Consider two ice skaters pushing off each other. Before they push off, their total momentum is zero (assuming they are at rest). After they push off, they move in opposite directions. The momentum of one skater moving to the right will be equal in magnitude and opposite in direction to the momentum of the other skater moving to the left, ensuring that the total momentum remains zero.
2. Impulse and Momentum: Impulse is defined as the change in momentum of an object when a force is applied over a period of time. The relationship between impulse (
) and momentum is given by:
![\[ J = \Delta p = F \Delta t \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-19917ccce6bf0fceaa558c166b018282_l3.png "Rendered by QuickLaTeX.com")
Where 
is the force applied and 
is the time duration over which the force acts.
Illustrative Explanation
Imagine a baseball player hitting a ball with a bat. The force exerted by the bat on the ball over the short time it contacts the ball results in a change in the ball’s momentum. The greater the force or the longer the contact time, the greater the change in momentum, which translates to a faster-moving ball after the hit.
3. Real-World Applications: Understanding momentum is essential in various real-world applications, including vehicle safety design, sports, and robotics. Engineers use momentum principles to design safer cars that can absorb impact during collisions, ensuring that passengers are protected.
Illustrative Explanation
In car crash tests, engineers analyze how momentum changes during a collision. By understanding the momentum of the car before and after the crash, they can design crumple zones that absorb energy and reduce the momentum transferred to passengers, thereby minimizing injuries.
Conclusion
In conclusion, the unit of momentum is a fundamental concept in physics that describes the quantity of motion an object possesses. Understanding the definition, mathematical representation, unit of momentum, significance, and illustrative explanations of momentum is essential for analyzing the motion of objects in various contexts. From the conservation of momentum to real-world applications in engineering and sports, momentum plays a vital role in our understanding of motion. By appreciating the intricacies of momentum, we can better navigate its implications in both scientific and practical contexts.